7  Confidence Intervals

7.1 Confidence Intervals

The sampling distribution describes how the statistic varies across samples. The confidence interval is a way to turn knowledge about that sampling distribution into a statement about the unknown parameter. A \(Z\%\) confidence interval for the mean implies that \(Z\%\) of the intervals we generate will contain the population mean, \(\mu\).

Note that a \(Z\%\) confidence interval does not imply a \(Z\%\) probability that the true parameter lies within a particular calculated interval. The interval you computed either contains the true mean or it does not.

In practice, people often interpret confidence intervals informally as “showing the uncertainty around our estimate”: wider intervals correspond to higher sampling variability and less precise information about \(\mu\). Just as with standard errors, we can estimate confidence intervals using theory-driven or data-driven approaches. We will focus on data-driven approaches first.

Computation.

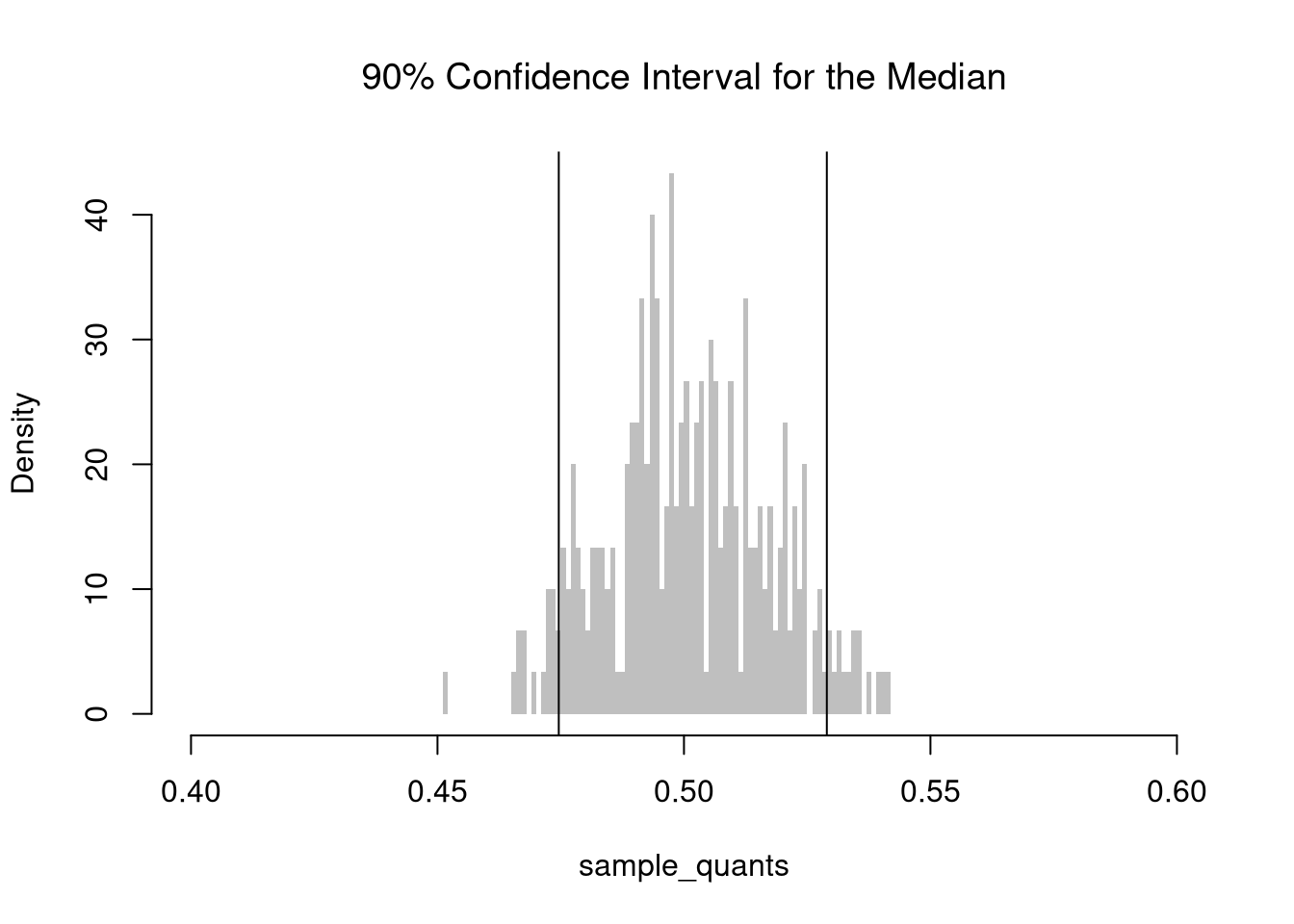
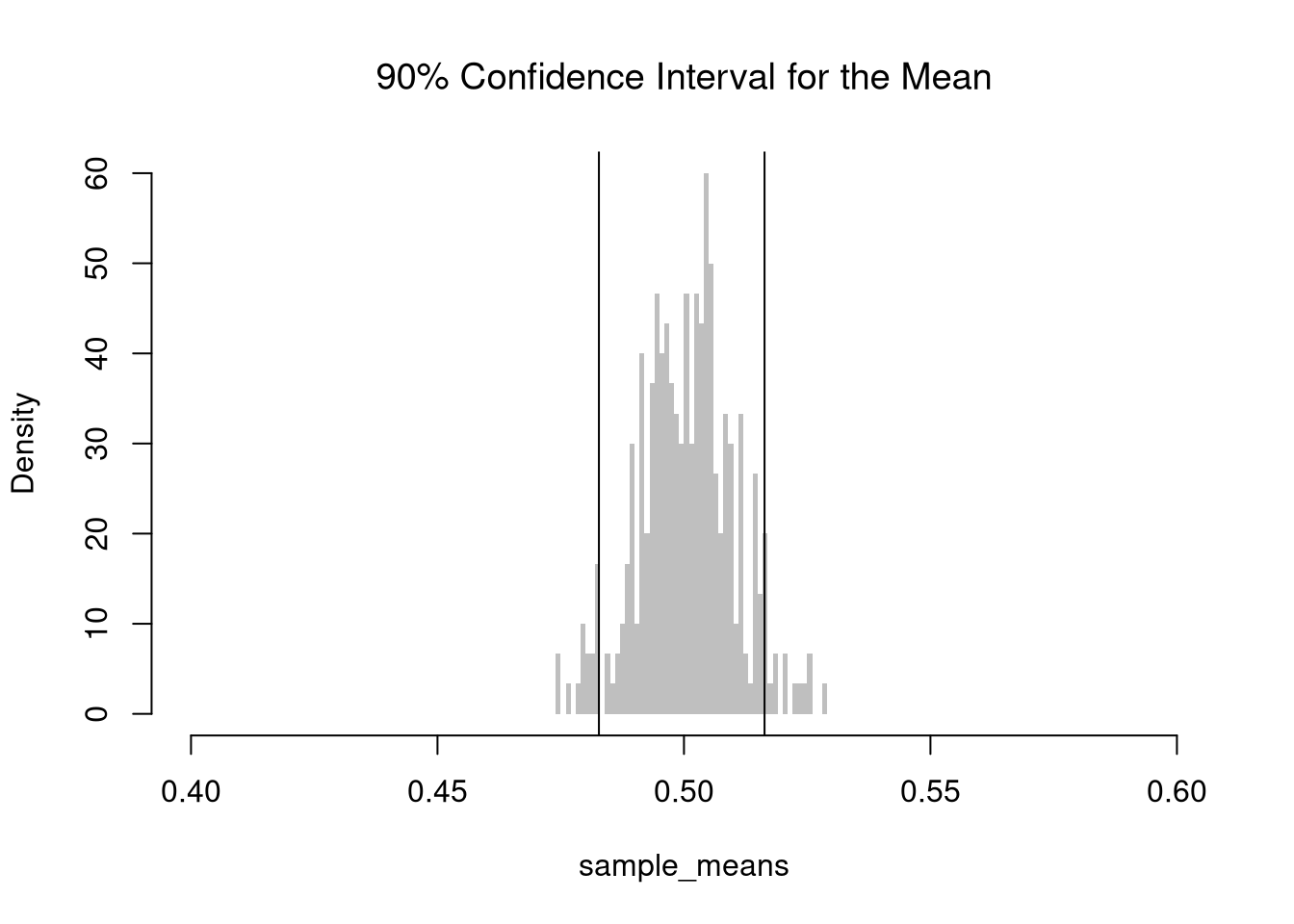
For example, consider the sample mean. We simulate the sampling distribution of the sample mean and construct a \(90\%\) confidence interval by taking the \(5^{th}\) and \(95^{th}\) percentiles of the sampling distribution. We then expect that approximately \(95\%\) of our constructed confidence intervals contain the theoretical population mean.

For example, consider the mean of a uniform random sample with a sample size of \(n=1000\).

Code 
# Create 300 samples, each with 1000 random uniform variables
x_samples <- matrix(nrow=300, ncol=1000)
for(i in seq(1,nrow(x_samples))){
    x_samples[i,] <- runif(1000)
}
sample_means <- apply(x_samples, 1, mean) # mean for each sample (row)

# Middle 90%
mq <- quantile(sample_means, probs=c(.05,.95))
paste0('we are 90% confident that the mean is between ', 
    round(mq[1],2), ' and ', round(mq[2],2) )
## [1] "we are 90% confident that the mean is between 0.48 and 0.51"

hist(sample_means,
    breaks=seq(.4,.6, by=.001), 
    border=NA, freq=F,
    col=rgb(0,0,0,.25), font.main=1,
    main='90% Confidence Interval for the Mean')
abline(v=mq)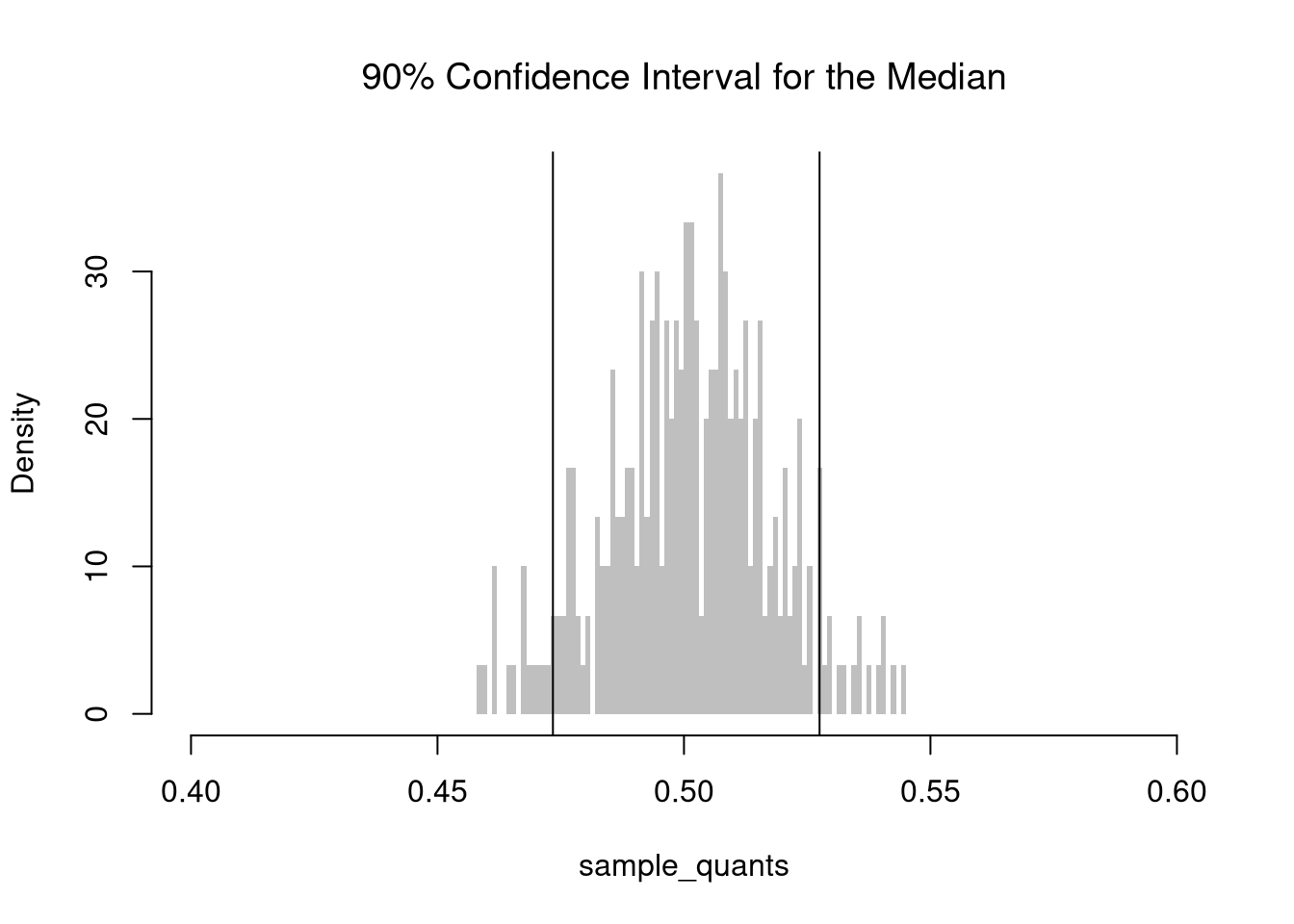

For another example, consider the median. We now repeat the above process to estimate the median for each sample, instead of the mean.

Code 
## Sample Quantiles (medians)
sample_quants <- apply(x_samples, 1, quantile, probs=0.5) #quantile for each sample (row)

# Middle 90% of estimates
mq <- quantile(sample_quants, probs=c(.05,.95))
paste0('we are 90% confident that the median is between ', 
    round(mq[1],2), ' and ', round(mq[2],2) )
## [1] "we are 90% confident that the median is between 0.48 and 0.52"

hist(sample_quants,
    breaks=seq(.4,.6, by=.001),
    border=NA, freq=F,
    col=rgb(0,0,0,.25), font.main=1,
    main='90% Confidence Interval for the Median')
abline(v=mq)

The \(5^{th}\) and \(95^{th}\) percentiles are called the “critical values” for the \(90\%\) confidence interval. The \(2.5^{th}\) and \(97.5^{th}\) percentiles are the critical values for the \(95\%\) confidence interval.

Interval Size.

Confidence intervals shrink with more data, as averaging washes out random fluctuations. Here is the intuition for estimating the weight of an apple:

  • With \(n=1\) apple, your estimate depends entirely on that one draw. If it happens to be unusually large or small, your estimate can be far off.
  • With \(n=2\) apples, the estimate averages out their idiosyncrasies. An unusually heavy apple can be balanced by a lighter one, lowering how far off you can be. You are less likely to get two extreme values than just one.
  • With \(n=100\) apples, individual apples barely move the needle. The average becomes stable.
Code 
# Create 300 samples, each of size n
par(mfrow=c(1,3))
for(n in c(25, 100, 250)){
x_samples <- matrix(nrow=300, ncol=n)
for(i in seq(1,nrow(x_samples))){
    x_samples[i,] <- runif(n)
}
# Compute means for each row (for each sample)
sample_means <- apply(x_samples, 1, mean)
# 90% Confidence Interval
mq <- quantile(sample_means, probs=c(.05,.95))
paste0('we are 90% confident that the mean is between ', 
    round(mq[1],2), ' and ', round(mq[2],2) )
hist(sample_means,
    breaks=seq(.1,.9, by=.005), 
    border=NA, freq=F, 
    col=rgb(0,0,0,.25), font.main=1,
    main=paste0('n=',n))
abline(v=mq)
}

Here is an intuitive example, from a small discrete population. Notice the extreme values

Code 
X <- c(18,20,22,24) #student ages (population values)
# six possible samples of size 2
m1 <- mean( X[c(1,2)] ) #{1,2}
m2 <- mean( X[c(1,3)] ) #{1,3}
m3 <- mean( X[c(1,4)] ) #{1,4}
m4 <- mean( X[c(2,3)] ) #{2,3}
m5 <- mean( X[c(2,4)] ) #{2,4}
m6 <- mean( X[c(3,4)] ) #{3,4}
means_2 <- c(m1, m2, m3, m4, m5, m6)
sort(means_2)
## [1] 19 20 21 21 22 23

# four possible samples of size 3
m1 <- mean( X[c(1,2,3)] ) 
m2 <- mean( X[c(1,2,4)] ) 
m3 <- mean( X[c(1,3,4)] ) 
m4 <- mean( X[c(2,3,4)] ) 
means_3 <- c(m1, m2, m3, m4)
sort(means_3)
## [1] 20.00000 20.66667 21.33333 22.00000

For a fixed sample size \(n\), there is a trade-off between precision: the width of a confidence interval, and accuracy: the probability that a confidence interval contains the theoretical value.

Resampling Intervals.

Often, we have only one sample. In practice, we can use resampling procedures to estimate a confidence interval. E.g., we repeatedly resample data and construct a bootstrap or jackknife sampling distribution. Then we compute the confidence intervals using the upper and lower quantiles of the sampling distribution.

Code 
sample_dat <- USArrests[,'Murder']
sample_mean <- mean(sample_dat)
sample_mean
## [1] 7.788

# Jackknife Distribution
n <- length(sample_dat)
jackknife_means <- vector(length=n)
for(i in seq_along(jackknife_means)){
    dat_noti <- sample_dat[-i]
    mean_noti <- mean(dat_noti)
    jackknife_means[i] <- mean_noti
}

# Bootstrap Distribution
set.seed(1) # to be replicable
bootstrap_means <- vector(length=9999)
for(b in seq_along(bootstrap_means)){
    dat_id <- seq(1,n)
    boot_id <- sample(dat_id , replace=T)
    dat_b  <- sample_dat[boot_id] # c.f. jackknife
    mean_b <- mean(dat_b)
    bootstrap_means[b] <-mean_b
}

# Jack CI
jack_ci <- quantile(jackknife_means, probs=c(.025, .975))
jack_ci
##     2.5%    97.5% 
## 7.621582 7.904082

# Boot CI
boot_ci <- quantile(bootstrap_means, probs=c(.025, .975))
boot_ci
##   2.5%  97.5% 
## 6.6039 8.9420

# more conservative estimate
ci <- boot_ci

7.2 Hypothesis Testing

In this section, we test hypotheses using data-driven methods that assume much less about the data generating process. There are two main ways to conduct a hypothesis test to do so: inverting a confidence interval and imposing the null. The first treats the distribution of estimates directly; the second explicitly enforces the null hypothesis to evaluate how unusual the observed statistic is. Both approaches rely on the bootstrap: resampling the data to approximate sampling variability. The most typical case is hypothesizing about about the mean.

Invert a CI.

One main way to conduct hypothesis tests is to examine whether a confidence interval contains a hypothesized value. We then use this decision rule

  • reject the null if value falls outside of the interval
  • fail to reject the null if value falls inside of the interval

We typically use a \(95\%\) confidence interval to create a rejection region: the area that falls outside of the interval.

For example, suppose you hypothesize the mean is \(9\). You then construct a bootstrap distribution with \(95\%\) confidence interval, and find your hypothesized value falls outside of the confidence interval. Then, after accounting for sampling variability (which you estimate), it still seems extremely unlikely that the theoretical mean actually equals \(9\), so you reject that that hypothesis. (If the theoretical value landed in the interval, you would “fail to reject” the theoretical mean equals \(9\).)

Code 
hist(bootstrap_means, breaks=25,
    border=NA,
    freq=F,
    main='',
    xlab='Bootstrap Samples')
# CI
ci_95 <- quantile(bootstrap_means, probs=c(.025, .975))
abline(v=ci_95, lwd=2)
# H0: mean=9
abline(v=9, col=2, lwd=2)

The above procedure also generalizes to many other statistics. Perhaps the most informative additional statistics for spread or shape. E.g., you can conduct hypothesis tests for sd and IQR, or skew and kurtosis.

Code 
# Bootstrap Distribution for SD
sd_obs <- sd(sample_dat)
bootstrap_sd <- vector(length=999)
for(b in seq_along(bootstrap_sd)){
    x_b <- sample(sample_dat, replace=T)
    sd_b <- sd(x_b)
    bootstrap_sd[b] <- sd_b
}

# Test for SD Differences (Invert CI)
sd_null <- 3.6
hist(bootstrap_sd, freq=F,
    border=NA, xlab='Bootstrap', font.main=1,
    main='Standard Deviations (Invert CI)')
sd_ci <- quantile(bootstrap_sd, probs=c(0.025,.975) )
abline(v=sd_ci, lwd=2)
abline(v=sd_null, lwd=2, col=2)

To better your understanding, try redoing the above for any function (such as IQR(x_b)/median(x_b))

Suppose you scored \(83\%\) on your exam with \(50\) questions, but think you are really a \(90\%\) student. Explain how you might test your hypothesis to your professor who insists your claim be supported by evidence. What would be the issue if we could not reject your hypothesis? Provide a computer simulation illustrating the issue.

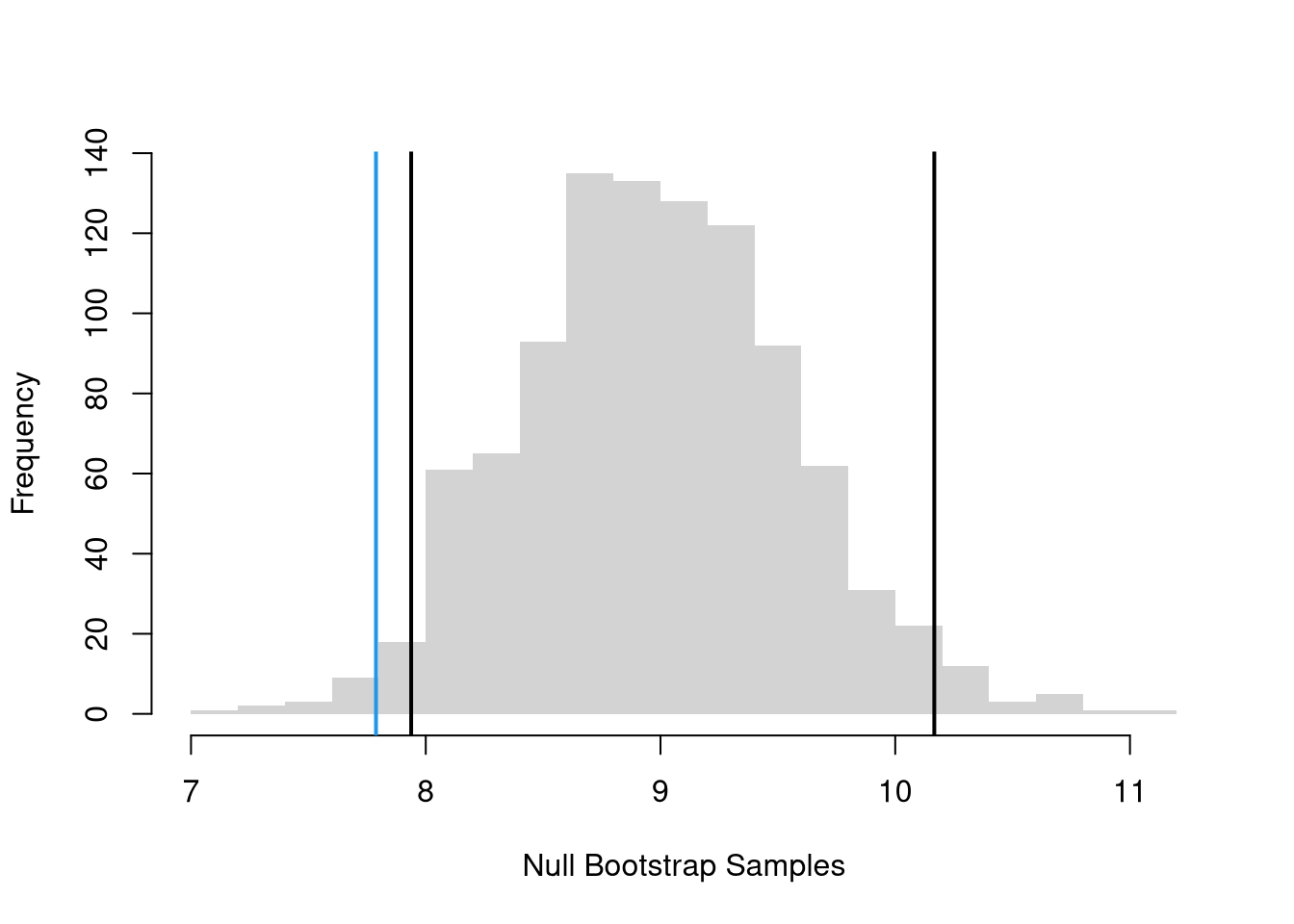
Impose the Null.

We can also compute a null distribution: the sampling distribution of the statistic under the null hypothesis (assuming your null hypothesis was true). We use the bootstrap to loop through a large number of “resamples”. In each iteration of the loop, we impose the null hypothesis and re-estimate the statistic of interest. We then calculate the range of the statistic across all resamples and compare how extreme the original value we observed is.

For example, suppose you hypothesize the mean is \(9\). You then construct a \(95\%\) confidence interval around the null bootstrap distribution (resamples centered around \(9\)). If your sample mean falls outside of that interval, then even after accounting for sampling variability (which you estimate), it seems extremely unlikely that the theoretical mean actually equals \(9\), so you reject that that hypothesis. (If the sample mean landed in the interval, you would “fail to reject” the theoretical mean equals \(9\).)

Code 
sample_dat <- USArrests[,'Murder']
sample_mean <- mean(sample_dat)

# Bootstrap NULL: mean=9
# Bootstrap shift: center each bootstrap resample so that the distribution satisfies the null hypothesis on average.
set.seed(1)
mu <- 9
bootstrap_means_null <- vector(length=999)
for(b in seq_along(bootstrap_means_null)){
    dat_b <- sample(sample_dat, replace=T) 
    mean_b <- mean(dat_b) + (mu - sample_mean) # impose the null via Bootstrap shift
    bootstrap_means_null[b] <- mean_b
}
hist(bootstrap_means_null, breaks=25, border=NA,
    main='',
    xlab='Null Bootstrap Samples')
ci_95 <- quantile(bootstrap_means_null, probs=c(.025, .975)) # critical region
abline(v=ci_95, lwd=2)
abline(v=sample_mean, lwd=2, col=4)

7.3 Misc. Topics

Normal Approximation.

Given the sampling distribution is approximately normally, the usual confidence intervals are symmetric. For the sample mean \(M\), we can then construct the interval \([M - E, M + E]\), where \(E\) is a “margin of error” on either side of \(M\). A coverage level of \(1-\alpha\) means \(Prob( M - E < \mu < M + E)=1-\alpha\). I.e., if the same sampling procedure were repeated \(100\) times from the same population, approximately \(95\) of the resulting intervals would be expected to contain the true population mean.1 We can also compute from theory that the \(\pm 1.96~ SE(M)\) corresponds to the critical values of the Normal distribution, where \(SE(M)\) is estimated using the bootstrap distribution or theory (classical SEs: \(\hat{S}/\sqrt{n}\)).

Code 
# Bootstrap Distribution with Percentile CI
sd_est_boot <- sd(bootstrap_means)
hist(bootstrap_means, breaks=25,
    main='Percentile vs Normal 95% CIs',
    font.main=1, border=NA,
    freq=F, ylim=c(0,0.7),
    xlab=expression(hat(b)[b]))
boot_ci_percentile <- quantile(bootstrap_means, probs=c(.025,.975))
abline(v=boot_ci_percentile, lty=1)

# Normal Approximation with Bootstrap SEs
dx <- seq(5,10,by=0.01)
lines(dx, dnorm(dx,sample_mean,sd_est_boot), col="blue", lty=1)
boot_ci_normal <- qnorm(c(.025,.975), sample_mean, sd_est_boot) #sample_mean+c(-1.96, +1.96)*sd_est_boot
abline(v=boot_ci_normal, col="blue", lty=3)

# Normal Approximation with IID Theory SEs
classic_se <- sd(sample_dat)/sqrt(length(sample_dat))
lines(dx, dnorm(dx,sample_mean,classic_se), col="red", lty=1)
ci_normal <-  qnorm(c(.025,.975), sample_mean, classic_se) #sample_mean+c(-1.96, +1.96)*classic_se
abline(v=ci_normal, col="red", lty=3)

Code 

paste0('Bootstrap SE = ', round(sd_est_boot,3))
## [1] "Bootstrap SE = 0.6"
paste0('Class SE = ', round(classic_se,3))
## [1] "Class SE = 0.616"

The main advantage and disadvantage of the Normal approximation is that it works well for estimating extreme probabilities, where resampling methods tend to be worse, but the sampling distribution might be far from normal. In the example above, they are all quite similar, but that does not always need to be the case.

This Normal based interval can also provide an alternative to the Null Bootstrap. While we could also use a Null Jackknife distribution, that is rarely done. Altogether, there are two different types of confidence intervals that “impose the null”.

Types of Confidence Interval Estimates that “impose the null”
Interval Mechanism
Bootstrap Percentile randomly resample \(n\) observations with replacement and shift
Normal assume observations are i.i.d. and normal distribution is a good approximation (can use bootstrap or classical SE’s)
Code 
# Confidence Interval for each sample
xq <- apply(x_samples, 1, function(r){ #theoretical se's 
    mean(r) + c(-1,1)*sd(r)/sqrt(length(r))
})
# First 3 interval estimates
xq[, c(1,2,3)]
##           [,1]      [,2]      [,3]
## [1,] 0.4639178 0.4999675 0.4832245
## [2,] 0.5011281 0.5363727 0.5178519

# Explicit calculation
mu_true <- 0.5 # theoretical result for uniform samples
# Logical vector: whether the true mean is in each CI
covered <- mu_true >= xq[1, ] & mu_true <= xq[2, ]
# Empirical coverage rate
coverage_rate <- mean(covered)
cat(sprintf("Estimated coverage probability: %.2f%%\n", 100 * coverage_rate))
## Estimated coverage probability: 69.00%

# Theoretically: [-1 sd, +1 sd] has 2/3 coverage
# Change to [-2 sd, +2 sd] to see Precision-Accuracy tradeoff.

Prediction Intervals.

Note that \(Z\%\) confidence intervals do not generally cover \(Z\%\) of the data (those types of intervals are covered later). In the examples above, notice the confidence interval for the mean differs from the confidence interval of the median, and so both cannot cover \(90\%\) of the data. The confidence interval for the mean is roughly \([0.48, 0.52]\), which theoretically covers only a \(0.52-0.48=0.04\) proportion of uniform random data, much less than the proportion \(0.9\).

In addition to confidence intervals, we can also compute a prediction interval which estimate the variability of new data rather than a statistic. To do so, we compute the frequency each value was covered.

Code 
x <- runif(1000)
# Middle 90% of values
xq0 <- quantile(x, probs=c(.05,.95))
paste0('we are 90% confident that the a future data point will be between ', 
    round(xq0[1],2), ' and ', round(xq0[2],2) )
## [1] "we are 90% confident that the a future data point will be between 0.04 and 0.95"

hist(x,
    breaks=seq(0,1,by=.01), border=NA,
    main='Prediction Interval', font.main=1)
abline(v=xq0)

7.4 Further Reading

See

  1. Notice that \(Prob( M - E < \mu < M + E) = Prob( - E < \mu - M < + E) = Prob( \mu + E > M > \mu - E)\). So if the interval \([\mu - 10, \mu + 10]\) contains \(95\%\) of all \(M\), then the interval \([M-10, M+10]\) will also contain \(\mu\) in \(95\%\) of the samples because whenever \(M\) is within \(10\) of \(\mu\), the value \(\mu\) is also within \(10\) of \(M\). But for any particular sample, the interval \([\hat{M}-10, \hat{M}+10]\) either does or does not contain \(\mu\). Similarly, if you compute \(\hat{M}=9\) for your particular sample, a coverage level of \(1-\alpha=95\%\) does not mean \(Prob(9 - E < \mu < 9 + E)=95\%\).↩︎