Often, we are interested in gradients: how \(Y\) changes with \(X\). The linear model depicts this as a simple constant, \(\hat{b}_{1}\), whereas other models do not. A great first way to assess gradients is to plot the predicted values over the explanatory values.
# Adaptive-width subsamples with non-uniform weights
xy <- USArrests[,c('UrbanPop','Murder')]
xy0 <- xy[order(xy[,'UrbanPop']),]
names(xy0) <- c('x','y')
plot(y~x, pch=16, col=grey(0,.5), dat=xy0)
reg_lo <- loess(y~x, data=xy0, span=.6)
red_col <- rgb(1,0,0,.5)
lines(xy0[,'x'], predict(reg_lo),
col=red_col, type='o', pch=2)
More formally, there are two ways to summarize gradients
For all methods, including regressograms, you can approximate gradients with small finite differences. For some small difference \(d\), we can manually compute \[\begin{eqnarray} \hat{b}_{1}(x) &=& \frac{ \hat{y}(x+\frac{d}{2}) - \hat{y}(x-\frac{d}{2})}{d}, \end{eqnarray}\]
When using split-sample regressions or local linear regressions, you can use the estimated slope coefficients \(\hat{b}_{1}(x)\) as gradient estimates in each direction.
After computing gradients, you can summarize them in various plots
## Gradients
pred_lo <- predict(reg_lo)
grad_x <- xy0[,'x'][-1]
grad_dx <- diff(xy0[,'x'])
grad_dy <- diff(pred_lo)
grad_lo <-grad_dy/grad_dx
## Visual Summary
par(mfrow=c(1,2))
hist(grad_lo, breaks=20,
border=NA, freq=F,
col=red_col,
xlab=expression(d~hat(y)/dx),
main='') ## Distributional Summary
plot(grad_x+grad_dx, grad_lo,
xlab='x', ylab=expression(d~hat(y)/dx),
col=red_col, pch=16) ## Diminishing Returns?
You may also be interested in a particular gradient or a single summary statistic. For example, a bivariate regressogram can estimate the “marginal effect at the mean”; \(\hat{b}_{1}( x=\hat{M}_{X} )\). More typically, you would be interested in the “mean of the gradients”, sometimes said simply as “average effect”, which averages the gradients over all datapoints in the dataset: \(1/n \sum_{i}^{n} \hat{b}_{1}(x=\hat{X}_{i})\). Alternatively, you may be interested in the median of the gradients, or measures of “effect heterogeneity”: the interquartile range or standard deviation of the gradients. Such statistics are single numbers that can be presented in tabular form: “mean gradient (sd gradient)”. You can alternative report standard errors: “mean gradient (estimated se), sd gradient (estimated se)”.
## Tabular Summary
tab_stats <- c(
M=mean(grad_lo, na.rm=T),
S=sd(grad_lo, na.rm=T))
tab_stats
## M S
## 0.01554515 0.16296598
## Use bootstrapping to get SE's
boot_stats <- matrix(NA, nrow=299, ncol=2)
colnames(boot_stats) <- c('M se', 'S se')
for(b in 1:nrow(boot_stats)){
xy_b <- xy0[sample(1:nrow(xy0), replace=T),]
reg_lo <- loess(y~x, data=xy_b, span=.6)
pred_lo <- predict(reg_lo)
grad_lo <- diff(pred_lo)/diff(xy_b[,'x'])
dydx_mean <- mean(grad_lo, na.rm=T)
dydx_sd <- sd(grad_lo, na.rm=T)
boot_stats[b,1] <- dydx_mean
boot_stats[b,2] <- dydx_sd
}
apply(boot_stats, 2, sd)
## M se S se
## 0.05145608 0.06862386Just as before, there are diminishing returns to larger sample sizes for bivariate statistics. For example, the slope coefficient in simple OLS varies less from sample to sample when the samples are larger. Same for the gradients in loess. This decreased variability across samples makes hypothesis testing more accurate.
B <- 300
Nseq <- seq(10,50, by=1)
SE <- sapply(Nseq, function(n){
sample_stat <- sapply(1:B, function(b){
x <- rnorm(n)
e <- rnorm(n)
y <- x*3 + x + e
reg_lo <- loess(y~x)
pred_lo <- predict(reg_lo)
grad_lo <- diff(pred_lo)/diff(x)
dydx_mean <- mean(grad_lo, na.rm=T)
#dydx_sd <- sd(grad_lo, na.rm=T)
return(dydx_mean)
})
sd(sample_stat)
})
plot(Nseq, SE, pch=16, col=grey(0,.5),
main='Mean gradient', font.main=1,
ylab='standard error',
xlab='sample size')
When we test a hypothesis, we start with a claim called the null hypothesis \(H_0\) and an alternative claim \(H_A\). Because we base conclusions on sample data, which has variability, mistakes are possible. There are two types of errors:
| True Situation | Decision: Fail to Reject \(H_0\) | Decision: Reject \(H_0\) |
|---|---|---|
| \(H_0\) is True | Correct (no detection) | Type I Error (False Positive) |
| \(H_0\) is False | Type II Error (False Negative; missed detection) | Correct (effect detected) |
The probability of Type I Error is called significance level and denoted by \(Prob(\text{Type I Error}) = \alpha\). The probability of correctly rejecting a false null is called power and denoted by \(\text{Power} = 1 - \beta = 1 - Prob(\text{Type II Error})\).
Significance is often chosen by statistical analysts to be \(\alpha=0.05\). Power is less often chosen, instead following from a decision about power.
There is an important Trade-off for fixed sample sizes: Increasing significance (fewer false positive) often lowers power (more false negatives). Generally, power depends on the effect size and sample size: bigger true effects and larger \(n\) make it easier to detect real differences (higher power, lower \(\beta\)).
Understanding whether we aim to describe, explain, or predict is central to empirical analysis. The three distinct purposes are to accurately describe empirical patterns, explain why the empirical patterns exist, predict what empirical patterns will exist.
| Objective | Core Question | Goal | Methods |
|---|---|---|---|
| Describe | What is happening? | Characterize patterns & facts | Summary stats, visualizations, correlations |
| Explain | Why is it happening? | Establish causal relationships & mechanisms | Theoretical models; experimentation; counterfactual reasoning |
| Predict | What will happen? | Anticipate outcomes; support decisions that affect the future | Machine learning, treatment effect forecasting, policy simulations |
Here is an example for minimum wages.
The distinctions matter, as they help you recognize that predictive accuracy or good data visualization does not equal causal insight. You can then better align statistical tools with questions. Try remembering this: Describe reality, Explain causes, Predict futures
In addition to confidence intervals, we can also compute a prediction interval which estimate the variability of new data rather than a statistic
In this example, we consider a single variable and compute the frequency each value was covered.
x <- runif(1000)
# Middle 90% of values
xq0 <- quantile(x, probs=c(.05,.95))
paste0('we are 90% confident that the a future data point will be between ',
round(xq0[1],2), ' and ', round(xq0[2],2) )
## [1] "we are 90% confident that the a future data point will be between 0.04 and 0.96"
hist(x,
breaks=seq(0,1,by=.01), border=NA,
main='Prediction Interval', font.main=1)
abline(v=xq0)
In this example, we consider a range for \(Y_{i}\) rather than for \(m(X_{i})\). These intervals also take into account the residuals, the variability of individuals rather than the variability of their mean.
# Bivariate Data from USArrests
xy <- USArrests[,c('Murder','UrbanPop')]
colnames(xy) <- c('y','x')
xy0 <- xy[order(xy[,'x']),]For a nice overview of different types of intervals, see https://www.jstor.org/stable/2685212. For an in-depth view, see “Statistical Intervals: A Guide for Practitioners and Researchers” or “Statistical Tolerance Regions: Theory, Applications, and Computation”. See https://robjhyndman.com/hyndsight/intervals/ for constructing intervals for future observations in a time-series context. See Davison and Hinkley, chapters 5 and 6 (also Efron and Tibshirani, or Wehrens et al.)
# From "Basic Regression"
xy0 <- xy[order(xy[,'x']),]
X0 <- unique(xy0[,'x'])
reg_lo <- loess(y~x, data=xy0, span=.8)
preds_lo <- predict(reg_lo, newdata=data.frame(x=X0))
# Jackknife CI
jack_lo <- sapply(1:nrow(xy), function(i){
xy_i <- xy[-i,]
reg_i <- loess(y~x, dat=xy_i, span=.8)
predict(reg_i, newdata=data.frame(x=X0))
})
boot_regs <- lapply(1:399, function(b){
b_id <- sample( nrow(xy), replace=T)
xy_b <- xy[b_id,]
reg_b <- lm(y~x, dat=xy_b)
})
plot(y~x, pch=16, col=grey(0,.5),
dat=xy0, ylim=c(0, 20))
lines(X0, preds_lo,
col=hcl.colors(3,alpha=.75)[2],
type='o', pch=2)
# Estimate Residuals CI at design points
res_lo <- sapply(1:nrow(xy), function(i){
y_i <- xy[i,'y']
preds_i <- jack_lo[,i]
resids_i <- y_i - preds_i
})
res_cb <- apply(res_lo, 1, quantile,
probs=c(.025,.975), na.rm=T)
# Plot
lines( X0, preds_lo +res_cb[1,],
col=hcl.colors(3,alpha=.75)[2], lt=2)
lines( X0, preds_lo +res_cb[2,],
col=hcl.colors(3,alpha=.75)[2], lty=2)
# Smooth estimates
res_lo <- lapply(1:nrow(xy), function(i){
y_i <- xy[i,'y']
x_i <- xy[i,'x']
preds_i <- jack_lo[,i]
resids_i <- y_i - preds_i
cbind(e=resids_i, x=x_i)
})
res_lo <- as.data.frame(do.call(rbind, res_lo))
res_fun <- function(x0, h, res_lo){
# Assign equal weight to observations within h distance to x0
# 0 weight for all other observations
ki <- dunif(res_lo[['x']], x0-h, x0+h)
ei <- res_lo[ki!=0,'e']
res_i <- quantile(ei, probs=c(.025,.975), na.rm=T)
}
res_lo2 <- sapply(X0, res_fun, h=15, res_lo=res_lo)
lines( X0, preds_lo + res_lo2[1,],
col=hcl.colors(3,alpha=.75)[2], lty=1, lwd=2)
lines( X0, preds_lo + res_lo2[2,],
col=hcl.colors(3,alpha=.75)[2], lty=1, lwd=2)
# Bootstrap Prediction Interval
boot_resids <- lapply(boot_regs, function(reg_b){
e_b <- resid(reg_b)
x_b <- reg_b[['model']][['x']]
res_b <- cbind(e_b, x_b)
})
boot_resids <- as.data.frame(do.call(rbind, boot_resids))
# Homoskedastic
ehat <- quantile(boot_resids[,'e_b'], probs=c(.025, .975))
x <- quantile(xy[,'x'],probs=seq(0,1,by=.1))
boot_pi <- coef(reg)[1] + x*coef(reg)['x']
boot_pi <- cbind(boot_pi + ehat[1], boot_pi + ehat[2])
# Plot Bootstrap PI
plot(y~x, dat=xy, pch=16, main='Prediction Intervals',
ylim=c(-5,20), font.main=1)
polygon( c(x, rev(x)), c(boot_pi[,1], rev(boot_pi[,2])),
col=grey(0,.2), border=NA)
# Parametric PI (For Comparison)
#pi <- predict(reg, interval='prediction', newdata=data.frame(x))
#lines( x, pi[,'lwr'], lty=2)
#lines( x, pi[,'upr'], lty=2)Perhaps the most common approach to selecting a bandwidth is to minimize error. Leave-one-out Cross-validation minimizes the average “leave-one-out” mean square prediction errors: \[\begin{eqnarray} \min_{h} \quad \frac{1}{n} \sum_{i=1}^{n} \left[ \hat{Y}_{i} - \hat{y_{[i]}}(X,h) \right]^2, \end{eqnarray}\] where \(\hat{y}_{[i]}(X,h)\) is the model predicted value at \(X_{i}\) based on a dataset that excludes \(X_{i}\), and \(h\) is the bandwidth (e.g., bin size in a regressogram).
Minimizing out-sample prediction error is perhaps the simplest computational approach to choose bandwidths, and it also addresses an issue that plagues observational studies in the social sciences: your model explains everything and predicts nothing. Note, however, minimizing prediction error is not necessarily “best”.
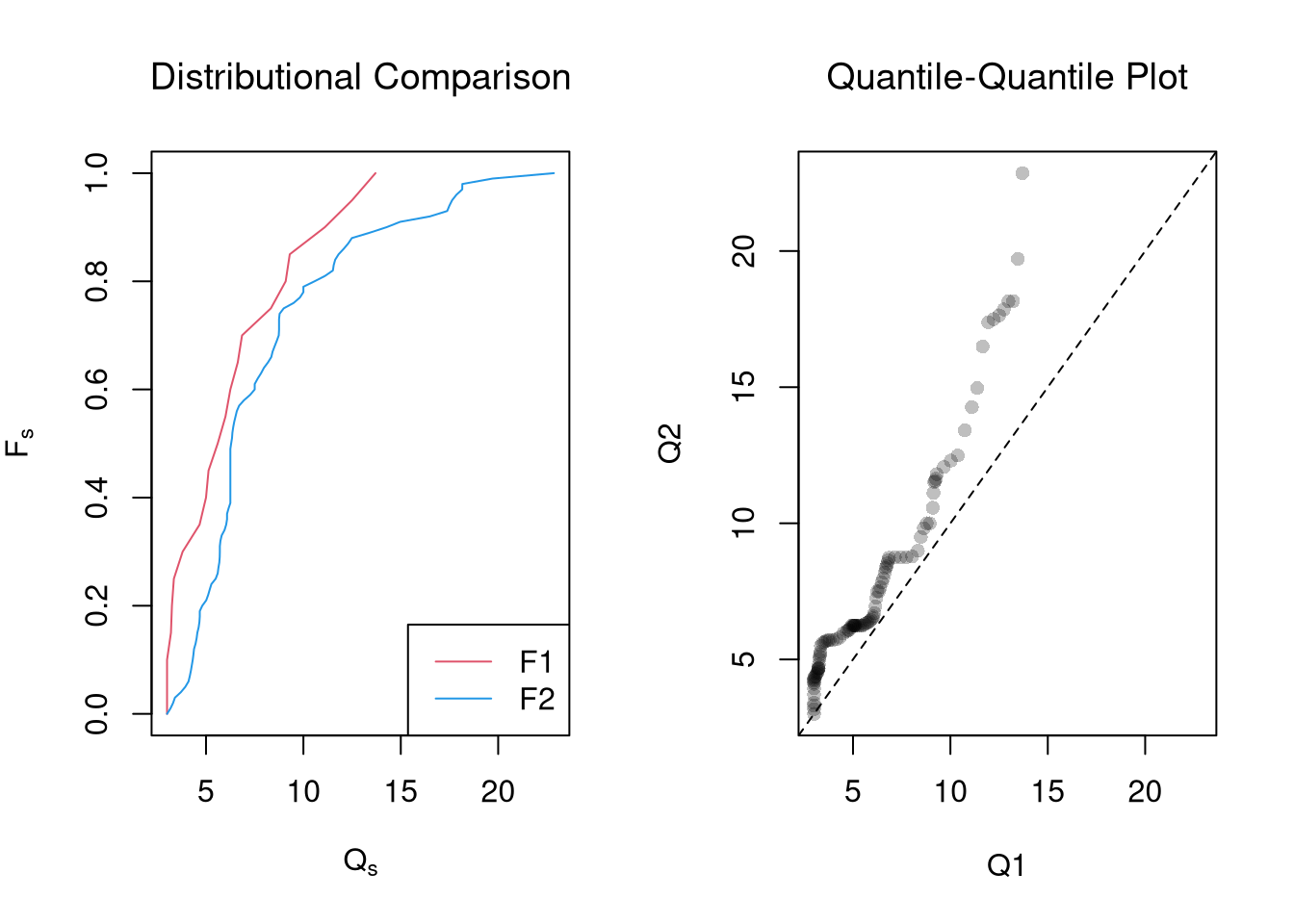
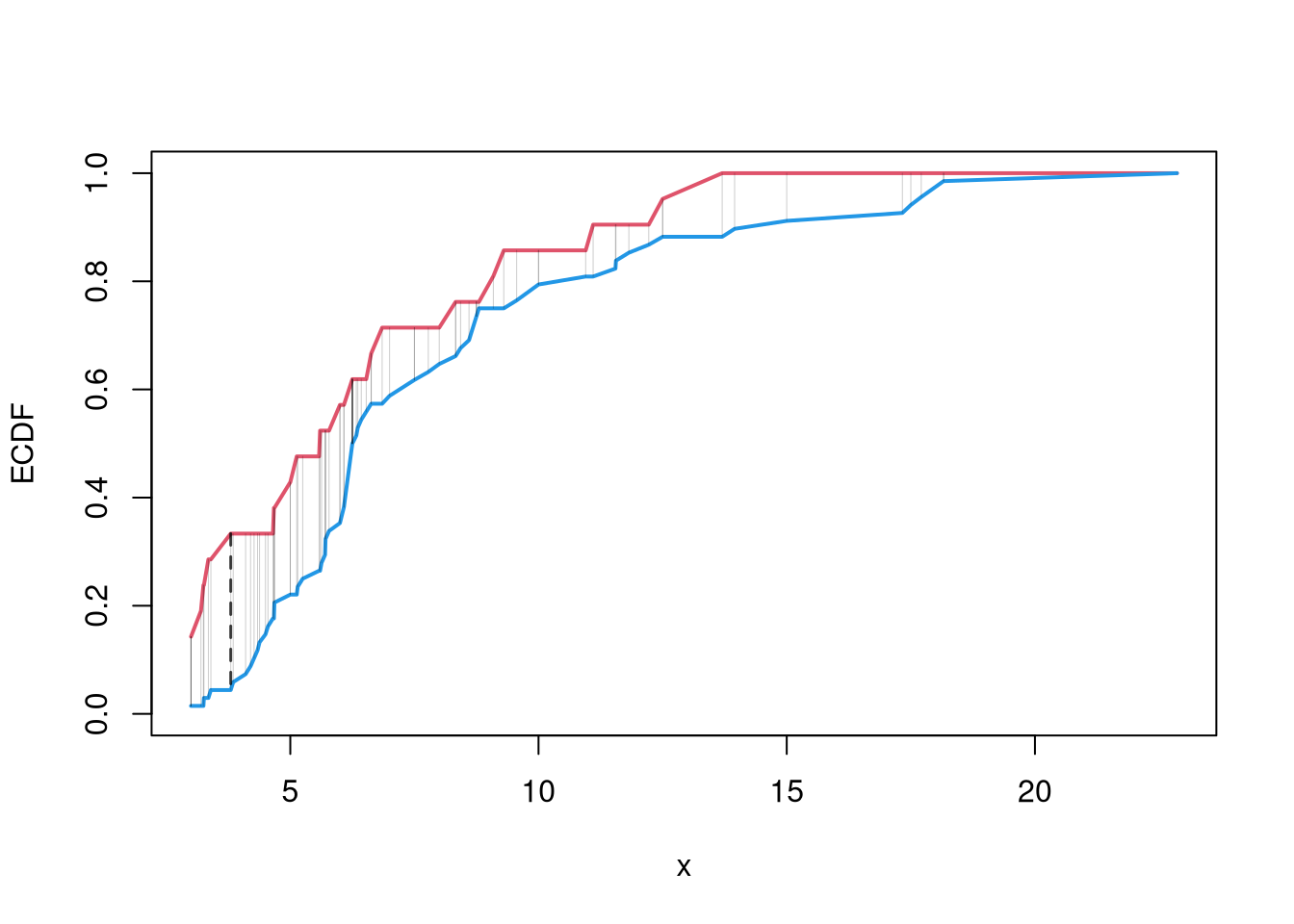
# Crossvalidated bandwidth for regression
xy_mat <- data.frame(y=CASchools[,'math'], x1=CASchools[,'income'])
library(np)
## Grid Search
BWS <- seq(1,10,length.out=20)
BWS_CV <- sapply(BWS, function(bw){
E_bw <- sapply(1:nrow(xy_mat), function(i){
llls <- npreg(y~x1, data=xy_mat[-i,],
bws=bw, regtype="ll",
ckertype='epanechnikov', bandwidth.compute=F)
pred_i <- predict(llls, newdata=xy_mat[i,])
e <- (pred_i- xy_mat[i,'y'])
return(e)
})
return( mean(E_bw^2) )
})
## Plot MSE
par(mfrow=c(1,2))
plot(BWS, BWS_CV, ylab='CV', pch=16,
xlab='bandwidth (h)',)
## Plot Resulting Predictions
bw <- BWS[which.min(BWS_CV)]
llls <- npreg(y~x1, data=xy_mat,
ckertype='epanechnikov',
bws=bw, regtype="ll")
plot(xy_mat[,'x'], predict(llls), pch=16, col=grey(0,.5),
xlab='X', ylab='Predictions')
abline(a=0,b=1, lty=2)
## Built in algorithmic Optimziation
llls2 <- npreg(y~x1, data=xy_mat, ckertype='epanechnikov', regtype="ll")
points(xy_mat[,'x'], predict(llls2), pch=2, col=rgb(1,0,0,.25))
## Add legend
add_legend <- function(...) {
opar <- par(fig=c(0, 1, 0, 1), oma=c(0, 0, 0, 0),
mar=c(0, 0, 0, 0), new=TRUE)
on.exit(par(opar))
plot(0, 0, type='n', bty='n', xaxt='n', yaxt='n')
legend(...)
}
add_legend('topright',
col=c(grey(0,.5),rgb(1,0,0,.25)),
pch=c(16,2),
bty='n', horiz=T,
legend=c('Grid Search', 'NP-algorithm'))# CV Application
## Smoothly Estimate X & Y Density
y <- sort(xy_mat[,'y'])
fy <- npudens(y, bandwidth.compute=TRUE)
x1 <- sort(xy_mat[,'x1'])
fx <- npudens(x1, bandwidth.compute=TRUE)
## Smoothly Estimate How Y changes with X
llls2 <- npreg(y~x1,data=xy_mat,
ckertype='epanechnikov',
regtype="ll", bandwidth.compute=TRUE)
layout( matrix(c(2,0,1,3), ncol=2, byrow=TRUE),
widths=c(4/5,1/5), heights=c(1/5,4/5))
## Joint Distribution
par(mar=c(4,4,1,1))
plot(y~x1, data=xy_mat,
pch=16, col=grey(0,.25),
xlab="District Income (1000$)",
ylab="Test Score")
lines( sort(xy_mat[,'x']), predict(llls2)[order(xy_mat[,'x1'])],
pch=16, col=1)
## Marginal Distribution
par(mar=c(0,4,1,1))
plot(x1, predict(fx),
col=grey(0,1), type='l', axes=F,
xlab='', ylab='')
rug(x1, col=grey(0,.25))
par(mar=c(4,0,1,1))
plot(predict(fy), y,
col=grey(0,1), type='l', axes=F,
xlab='', ylab='')
rug(y, col=grey(0,.25), side=2)