20 Experimental Data

20.1 Design Basics

Control and Randomize.

Perhaps the main feature that distinguishes experimental data from observational data is “control”. You can manipulate one of the explanatory variables, and also ensure that other factors are not changing at the same time.

Another distinguishing feature of experiments is “randomization”. You can ensure that a manipulated variable is not systematically associated with other variables.

To be concrete, we will continue with our supply and demand example from the last chapter, and this time introduce a cost shock.

Competitive Equilibrium Example.

Code

# Demand Curve Simulator
qd_fun <- function(p, Ad=8, Bd=-.8, Ed_sigma=.25){
    Qd <- Ad + Bd*p + rnorm(1,0,Ed_sigma)
    return(Qd)
}

# Supply Curve Simulator
qs_fun <- function(p, As=-8, Bs=1, Es_sigma=.25){
    Qs <- As + Bs*p + rnorm(1,0,Es_sigma)
    return(Qs)
}

# Quantity Supplied and Demanded at 3 Prices
cbind(P=8:10, D=qd_fun(8:10), S=qs_fun(8:10))
##       P          D          S
## [1,]  8 1.68508047 -0.2082764
## [2,]  9 0.88508047  0.7917236
## [3,] 10 0.08508047  1.7917236

# Market Equilibrium Finder
eq_fun <- function(demand, supply, P){
    # Compute EQ (what we observe)
    eq_id <- which.min( abs(demand-supply) )
    eq <- c(P=P[eq_id], Q=demand[eq_id]) 
    return(eq)
}

Code

N <- 300 # Number of Market Interactions
P <- seq(5,10,by=.01) # Price Range to Consider
EQ1 <- sapply(1:N, function(n){
    # Market Data Generating Process
    demand <- qd_fun(P)
    supply <- qs_fun(P)
    eq <- eq_fun(demand, supply, P)    
    return(eq)
})
dat1 <- data.frame(t(EQ1), cost='1', T=1:N)

If you have exogenous variation on one side of the market, you can get information on the other. For example, lower costs shift out supply (more is produced at given price), allowing you to trace out part of a demand curve.

To see this, consider an experiment where student subjects are recruited to a classroom and randomly assigned to be either buyers or sellers in a market for little red balls. In this case, the classroom environment allows the experimenter to control for various factors (e.g., the temperature of the room is constant for all subjects) and the explicit randomization of subjects means that there are not typically systematic differences in different groups of students.

In the experiment, sellers are given linear “cost functions” that theoretically yield individual supplies like \(\eqref{eqn:market_supply}\) and are paid “price - cost”. Buyers are given linear “benefit functions” that theoretically yield individual demands like \(\eqref{eqn:market_demand}\), and are paid “benefit - price”. The theoretical predictions are theorefore given in \(\eqref{eqn:market_supply}\). Moreover, experimental manipulation of \(\alpha_{S}\) leads to \[\begin{eqnarray} \label{eqn:comp_market_statics} \frac{d P^{*}}{d \alpha_{S}} = \frac{-1}{\beta_{D}+\beta_{S}}, \\ \frac{d Q^{*}}{d \alpha_{S}} = \frac{\beta_{D}}{\beta_{D}+\beta_{S}}. \end{eqnarray}\] In this case, the supply shock has identified the demand slope: \(-\beta_{D}=d Q^{*}/d P^{*}\).

Code

# New Observations After Cost Change
EQ2 <- sapply(1:N, function(n){
    demand <- qd_fun(P)
    supply2 <- qs_fun(P, As=-6.5) # More Supplied at Given Price
    eq <- eq_fun(demand, supply2, P)
    return(eq)
    # lines(supply2, P, col=rgb(0,0,1,.01))
    #points(eq[2], eq[1], col=rgb(0,0,1,.05), pch=16)
})
dat2 <- data.frame(t(EQ2), cost='2', T=(1:N) + N)
dat2 <- rbind(dat1, dat2)

# Plot Simulated Market Data
cols <- ifelse(as.numeric(dat2$cost)==2, rgb(0,0,1,.2), rgb(0,0,0,.2))
plot.new()
plot.window(xlim=c(0,2), ylim=range(P))
points(dat2$Q, dat2$P, col=cols, pch=16)
axis(1)
axis(2)
mtext('Quantity',1, line=2)
mtext('Price',2, line=2)

If the function forms for supply and demand are different from what we predicted, we can still measure how much the experimental manipulation of production costs affects the equilibrium quantity sold (and compare that to what was predicted).¹

20.2 Comparisons Over Time

Regression Discontinuities/Kinks.

The basic idea of RDD/RKD is to examine how a variable changes just before and just after a treatment. RDD estimates the difference in the levels of an outcome variable, whereas RKD estimates the difference in the slope. Turning to our canonical competitive market example, the RDD estimate is the difference between the lines at \(T=300\).

Code

# Locally Linear Regression 
# (Compare means near break)

cols <- ifelse(as.numeric(dat2$cost)==2, rgb(0,0,1,.5), rgb(0,0,0,.5))
plot(P~T, dat2, main='Effect of Cost Shock on Price', 
    font.main=1, pch=16, col=cols)
regP1 <- loess(P~T, dat2[dat2$cost==1,]) 
x1 <- regP1$x
#lm(): x1 <- regP1$model$T 
lines(x1, predict(regP1), col=rgb(0,0,0), lwd=2)
regP2 <- loess(P~T, dat2[dat2$cost==2,])
x2 <- regP2$x #regP1$model$T
lines(x2, predict(regP2), col=rgb(0,0,1), lwd=2)

Code


plot(Q~T, dat2, main='Effect of Cost Shock on Quantity',
    font.main=1, pch=16, col=cols)
regQ1 <- loess(Q~T, dat2[dat2$cost==1,]) 
lines(x1, predict(regQ1), col=rgb(0,0,0), lwd=2)
regQ2 <- loess(Q~T, dat2[dat2$cost==2,])
x2 <- regP2$x #regP1$model$T
lines(x2, predict(regQ2), col=rgb(0,0,1), lwd=2)

Code

# Linear Regression Alternative
sub_id <- (dat2$cost==1 & dat2$T > 250) | (dat2$cost==2 & dat2$T < 300)
dat2W <- dat2[sub_id,  ]
regP <- lm(P~T*cost, dat2)
regQ <- lm(Q~T*cost, dat2)
stargazer::stargazer(regP, regQ, 
    type='html',
    title='Recipe RDD',
    header=F)

**Recipe RDD**

	Dependent variable:

	P	Q
	(1)	(2)

T	-0.0001	0.0001
	(0.0001)	(0.0001)

cost2	-0.706^***	0.628^***
	(0.065)	(0.054)

T:cost2	-0.0002	0.00003
	(0.0002)	(0.0002)

Constant	8.892^***	0.879^***
	(0.023)	(0.019)


Observations	600	600
R²	0.805	0.803
Adjusted R²	0.804	0.802
Residual Std. Error (df = 596)	0.199	0.165
F Statistic (df = 3; 596)	819.647^***	808.340^***

Note:	p<0.1; p<0.05; p<0.01

Remember that this is effect is local: different magnitudes of the cost shock or different demand curves generally yield different estimates.

Moreover, note that more than just costs have changed over time: subjects in the later periods have history experience behind them while they do not in earlier periods. So hidden variables like “beliefs” are implicitly treated as well. This is one concrete reason to have an explicit control group.

Difference in Differences.

The basic idea of DID is to examine how a variable changes in response to an exogenous shock, compared to a control group.

Code

EQ3 <- sapply(1:(2*N), function(n){

    # Market Mechanisms
    demand <- qd_fun(P)
    supply <- qs_fun(P)

    # Compute EQ (what we observe)
    eq_id <- which.min( abs(demand-supply) )
    eq <- c(P=P[eq_id], Q=demand[eq_id]) 

    # Return Equilibrium Observations
    return(eq)
})
dat3 <- data.frame(t(EQ3), cost='1', T=1:ncol(EQ3))
dat3_pre  <- dat3[dat3$T <= N ,]
dat3_post <- dat3[dat3$T > N ,]

# Plot Price Data
par(mfrow=c(1,2))
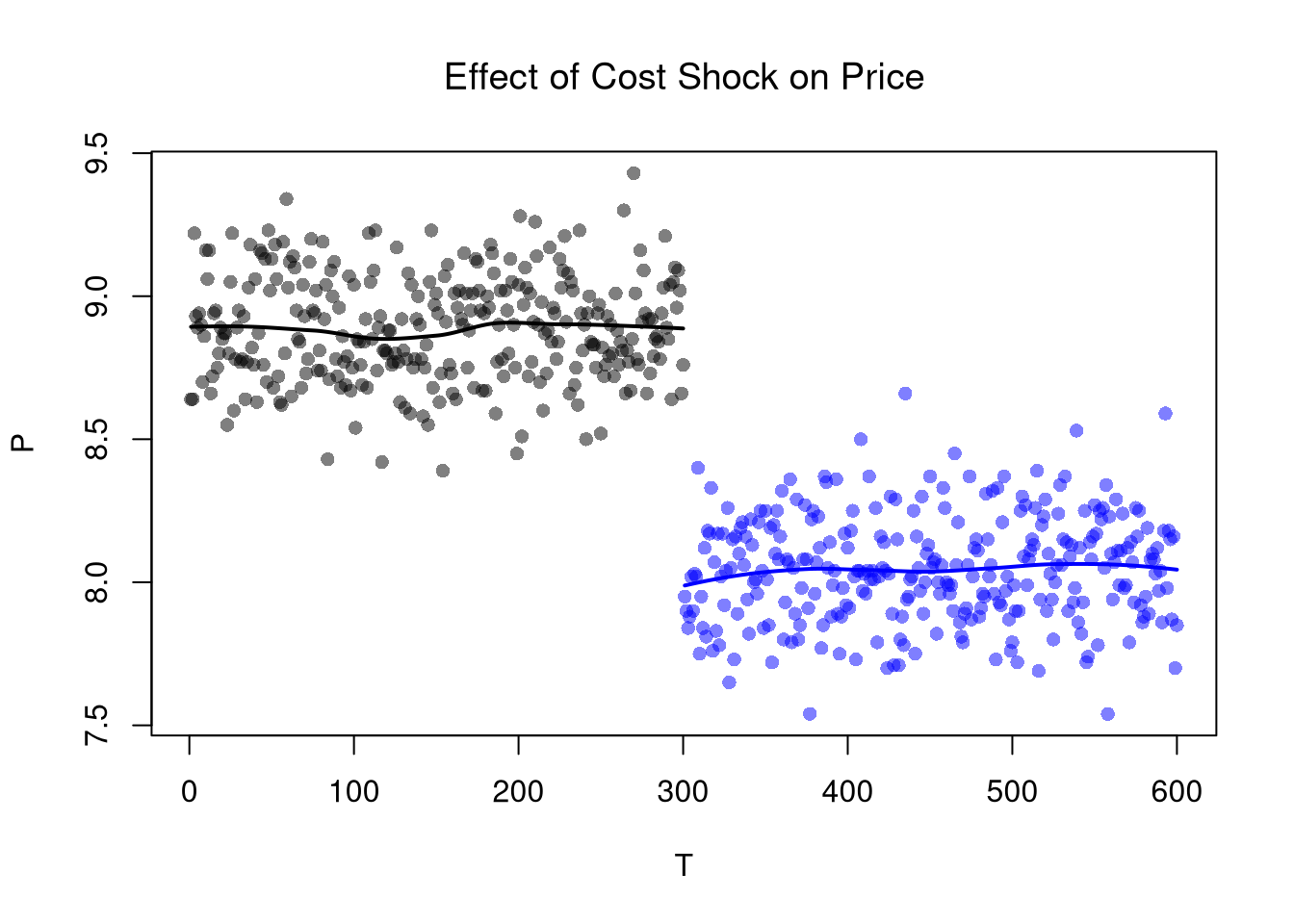
plot(P~T, dat2, main='Effect of Cost Shock on Price', 
    font.main=1, pch=16, col=cols, cex=.5)
lines(x1, predict(regP1), col=rgb(0,0,0), lwd=2)
lines(x2, predict(regP2), col=rgb(0,0,1), lwd=2)
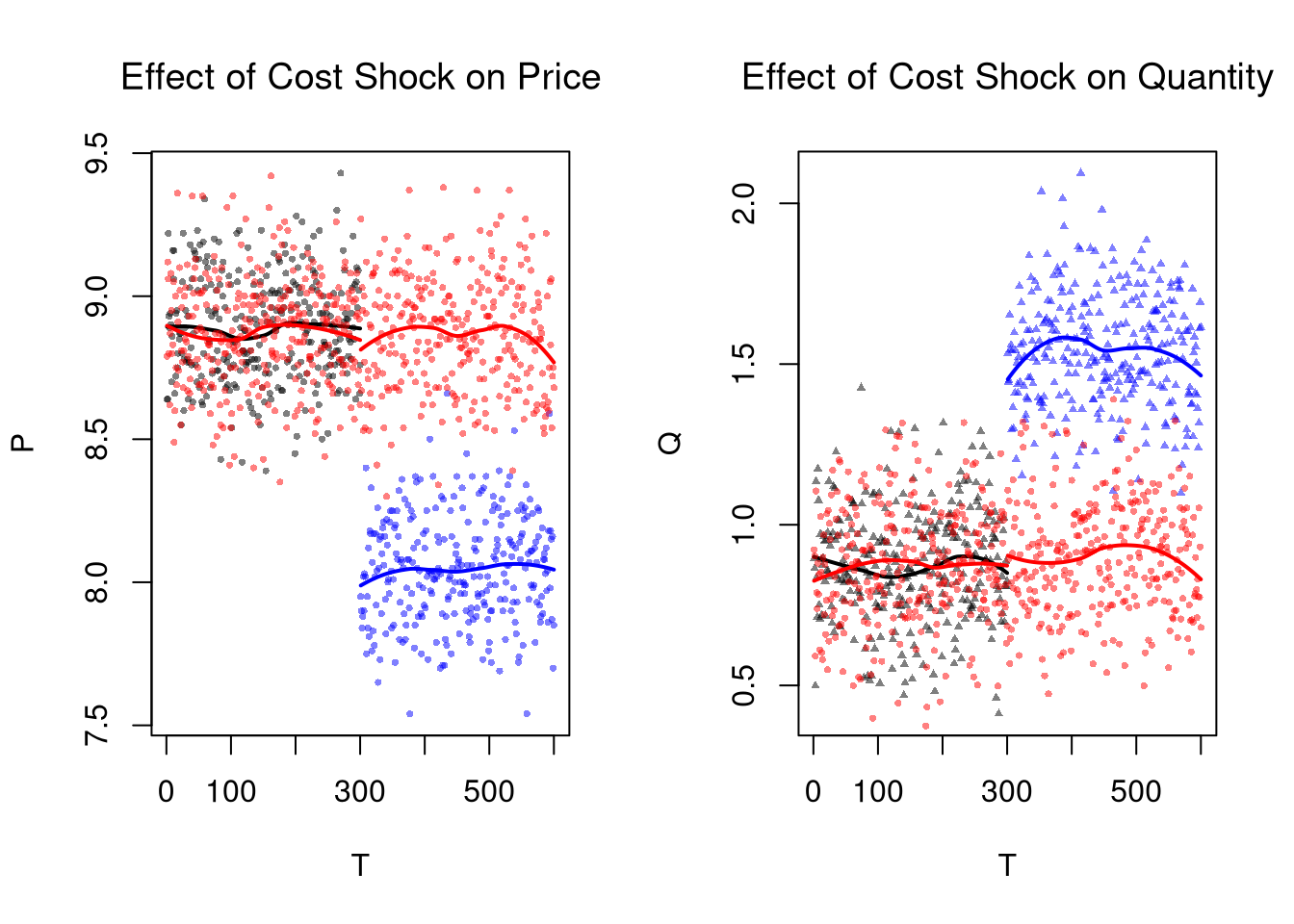
# W/ Control group
points(P~T, dat3, pch=16, col=rgb(1,0,0,.5), cex=.5)
regP3a <- loess(P~T, dat3_pre)
x3a <- regP3a$x
lines(x3a, predict(regP3a), col=rgb(1,0,0), lwd=2)
regP3b <- loess(P~T, dat3_post)
x3b <- regP3b$x
lines(x3b, predict(regP3b), col=rgb(1,0,0), lwd=2)


# Plot Quantity Data
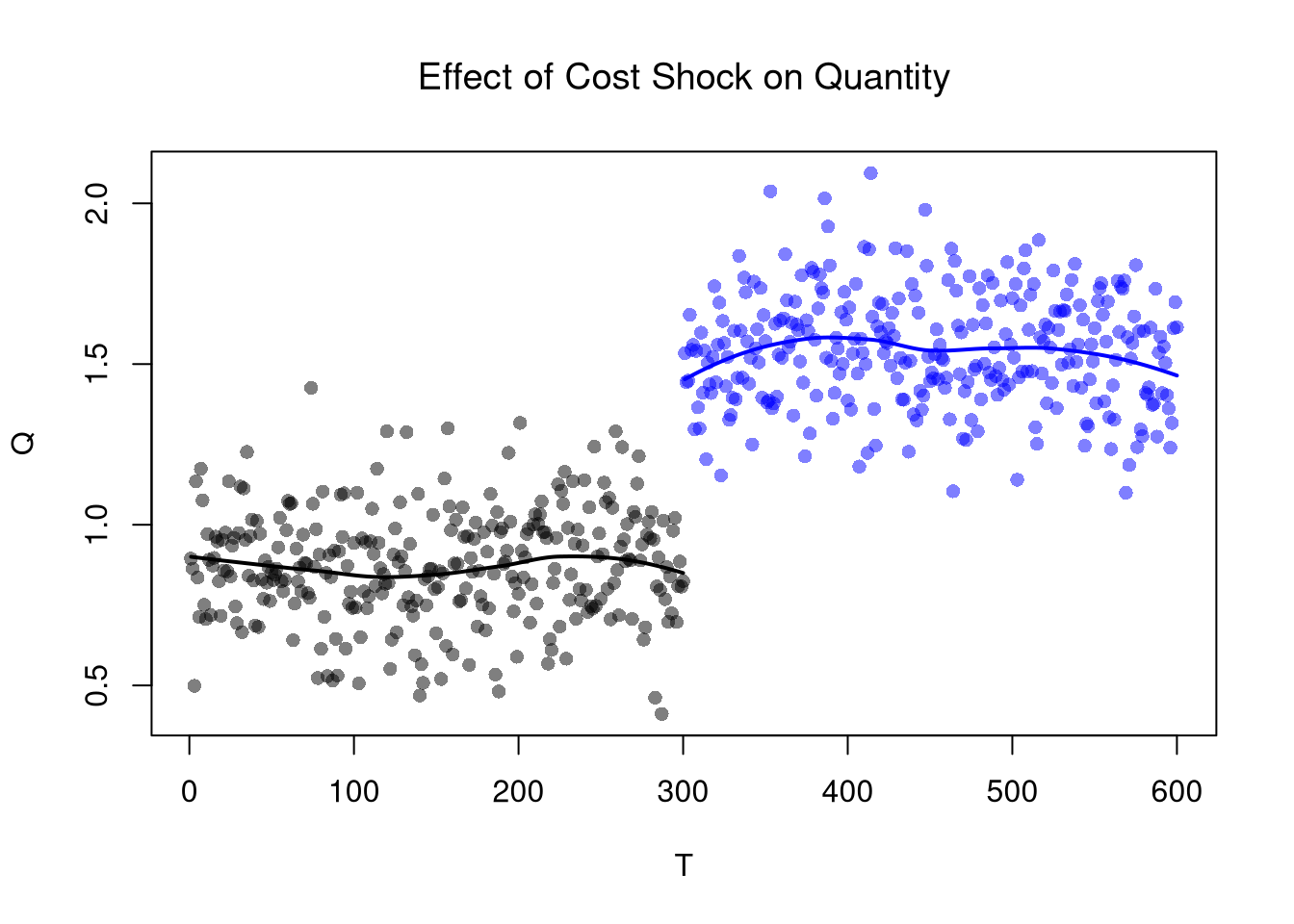
plot(Q~T, dat2, main='Effect of Cost Shock on Quantity',
    font.main=1, pch=17, col=cols, cex=.5)
lines(x1, predict(regQ1), col=rgb(0,0,0), lwd=2)
lines(x2, predict(regQ2), col=rgb(0,0,1), lwd=2)
# W/ Control group
points(Q~T, dat3, pch=16, col=rgb(1,0,0,.5), cex=.5)
regQ3a <- loess(Q~T, dat3_pre) 
lines(x3a, predict(regQ3a), col=rgb(1,0,0), lwd=2)
regQ3b <- loess(Q~T, dat3_post) 
lines(x3b, predict(regQ3b), col=rgb(1,0,0), lwd=2)

Linear Regression Estimates

Code

# Pool Data
dat_pooled <- rbind(
    cbind(dat2, EverTreated=1, PostPeriod=(dat2$T > N)),
    cbind(dat3, EverTreated=0, PostPeriod=(dat3$T > N)))
dat_pooled$EverTreated <- as.factor(dat_pooled$EverTreated)
dat_pooled$PostPeriod <- as.factor(dat_pooled$PostPeriod)

# Estimate Level Shift for Different Groups after T=300
regP <- lm(P~PostPeriod*EverTreated, dat_pooled)
regQ <- lm(Q~PostPeriod*EverTreated, dat_pooled)
stargazer::stargazer(regP, regQ, 
    type='html',
    title='Recipe DiD',
    header=F)

**Recipe DiD**

	Dependent variable:

	P	Q
	(1)	(2)

PostPeriod	-0.007	0.001
	(0.016)	(0.014)

EverTreated1	-0.004	0.001
	(0.016)	(0.014)

PostPeriodTRUE:EverTreated1	-0.799^***	0.662^***
	(0.022)	(0.020)

Constant	8.888^***	0.889^***
	(0.011)	(0.010)


Observations	1,200	1,200
R²	0.765	0.732
Adjusted R²	0.765	0.731
Residual Std. Error (df = 1196)	0.194	0.174
F Statistic (df = 3; 1196)	1,300.757^***	1,089.820^***

Note:	p<0.1; p<0.05; p<0.01

Blocking and Clustering .

Randomization is the process of randomly manipulating an explanatory variable of (assigning treatments to units).

A completely randomized design is useful when the experimental units are homogeneous. If the experimental units are heterogeneous, blocking is often used to form homogeneous groups.

Continuing with supply and demand example, we might manipulate costs (randomize high or low treatments) for companies in different industries (computer services, lumber harvesting).

20.3 Quasi Experiments

Quasi or “Natural” experiments are historical case studies have the second distinguishing feature of experiments: randomization, but not the first: control. This helps remedy the endogeneity issues in observational data. “Intrumental Variables”, “RDD”, “DID” methods discussed above are used in historical event studies. The elementary versions use linear regression, so I can cover them here using our competitive equilibrium example from before.

Two Stage Least Squares (2SLS).

Consider the market equilibrium example, which contains a cost shock. We can simply run another regression, but there will still be a problem.

Code

# Not exactly right, but at least right sign
reg2 <- lm(Q~P, data=dat2)
summary(reg2)
## 
## Call:
## lm(formula = Q ~ P, data = dat2)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.71544 -0.13923 -0.01042  0.15863  0.60378 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  6.73463    0.17518   38.44   <2e-16 ***
## P           -0.65011    0.02063  -31.52   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.227 on 598 degrees of freedom
## Multiple R-squared:  0.6242, Adjusted R-squared:  0.6236 
## F-statistic: 993.3 on 1 and 598 DF,  p-value: < 2.2e-16

It turns out that the noisiness of the process within each group affects our OLS estimate: \(\hat{B^{*}}=\hat{C}_{Q^{*}P^{*}} / \hat{V}_{P^{*}}\). For details, see

Within Group Variance

You can experiment with the effect of different variances on both OLS and IV in the code below. And note that if we had multiple supply shifts and recorded their magnitudes, then we could recover more information about demand, perhaps tracing it out entirely.

Code

# Examine
Egrid <- expand.grid(Ed_sigma=c(.001, .25, 1), Es_sigma=c(.001, .25, 1))

Egrid_regs <- lapply(1:nrow(Egrid), function(i){
    Ed_sigma <- Egrid[i,1]
    Es_sigma <- Egrid[i,2]    
    EQ1 <- sapply(1:N, function(n){
        demand <- qd_fun(P, Ed_sigma=Ed_sigma)
        supply <- qs_fun(P, Es_sigma=Es_sigma)
        return(eq_fun(demand, supply, P))
    })
    EQ2 <- sapply(1:N, function(n){
        demand <- qd_fun(P,Ed_sigma=Ed_sigma)
        supply2 <- qs_fun(P, As=-6.5,Es_sigma=Es_sigma)
        return(eq_fun(demand, supply2, P))
    })
    dat <- rbind(
        data.frame(t(EQ1), cost='1'),
        data.frame(t(EQ2), cost='2'))
    return(dat)
})
Egrid_OLS <- sapply(Egrid_regs, function(dat) coef( lm(Q~P, data=dat)))
Egrid_IV <- sapply(Egrid_regs, function(dat) coef( feols(Q~1|P~cost, data=dat)))

#cbind(Egrid, coef_OLS=t(Egrid_OLS)[,2], coef_IV=t(Egrid_IV)[,2])
lapply( list(Egrid_OLS, Egrid_IV), function(ei){
    Emat <- matrix(ei[2,],3,3)
    rownames(Emat) <- paste0('Ed_sigma.',c(.001, .25, 1))
    colnames(Emat) <- paste0('Es_sigma.',c(.001, .25, 1))
    return( round(Emat,2))
})

To overcome this issue, we can compute the change in the expected values \(d \mathbb{E}[Q^{*}] / d \mathbb{E}[P^{*}] =-\beta_{D}\). Empirically, this is estimated via the change in average value.

Code

# Wald (1940) Estimate
dat_mean <- rbind(
    colMeans(dat2[dat2$cost==1,1:2]),
    colMeans(dat2[dat2$cost==2,1:2]))
dat_mean
##             P         Q
## [1,] 8.883867 0.8898249
## [2,] 8.078167 1.5521779
B_est <- diff(dat_mean[,2])/diff(dat_mean[,1])
round(B_est, 2)
## [1] -0.82

We can also separately recover \(d \mathbb{E}[Q^{*}] / d \mathbb{E}[\alpha_{S}]\) and \(d \mathbb{E}[P^{*}] / d \mathbb{E}[\alpha_{S}]\) from separate regressions.²

Code

# Heckman (2000, p.58) Estimate
ols_1 <- lm(P~cost, data=dat2)
ols_2 <- lm(Q~cost, data=dat2)
B_est2 <- coef(ols_2)/coef(ols_1)
round(B_est2[[2]],2)
## [1] -0.82

Alternatively, we can recover the same estimate using an 2SLS regression with two equations: \[\begin{eqnarray} \hat{P} &=& b_{0p} + b_{1p} \alpha_{S} + e_{p} \\ \hat{Q} &=& b_{0q} + b_{1q} \hat{p} + e_{q}. \end{eqnarray}\] where \(\hat{p}\), the predicted value of \(\hat{P}\) from the first equation, is used to explain quantity in the second equation. In the first regression, we estimate how the cost shock affects prices: \(\hat{b}_{1p}\) and then predict prices \(\hat{p}\). In the second equation, we estimate how the average effect of predicted prices (which are exogenous to demand) affect quantity demanded.

To understand this theoretically, first substitute the equilibrium condition into the supply equation: \(Q_{D}=Q_{S}=\alpha_{S}+ \beta_{S} P + E_{S}\), lets us rewrite \(P\) as a function of \(Q_{D}\). This yields two theoretical equations. We are using the cost shock to understand the theoretical demand curve. \[\begin{eqnarray} \label{eqn:linear_supply_iv} P &=& -\frac{\alpha_{S}}{{\beta_{S}}} + \frac{Q_{D}}{\beta_{S}} - \frac{E_{S}}{\beta_{S}} \\ \label{eqn:linear_demand_iv} Q_{D} &=& \alpha_{D} + \beta_{D} P + E_{D}. \end{eqnarray}\]

Code

# Two Stage Least Squares Estimate
ols_1 <- lm(P~cost, data=dat2)
dat2_new  <- cbind(dat2, Phat=predict(ols_1))
reg_2sls <- lm(Q~Phat, data=dat2_new)
summary(reg_2sls)
## 
## Call:
## lm(formula = Q ~ Phat, data = dat2_new)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.43947 -0.10944  0.00566  0.11676  0.53412 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  8.19311    0.14170   57.82   <2e-16 ***
## Phat        -0.82208    0.01669  -49.26   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1647 on 598 degrees of freedom
## Multiple R-squared:  0.8023, Adjusted R-squared:  0.8019 
## F-statistic:  2426 on 1 and 598 DF,  p-value: < 2.2e-16

# One Stage Instrumental Variables Estimate
library(fixest)
reg2_iv <- feols(Q~1|P~cost, data=dat2)
summary(reg2_iv)
## TSLS estimation - Dep. Var.: Q
##                   Endo.    : P
##                   Instr.   : cost
## Second stage: Dep. Var.: Q
## Observations: 600
## Standard-errors: IID 
##              Estimate Std. Error  t value  Pr(>|t|)    
## (Intercept)  8.193109   0.206388  39.6975 < 2.2e-16 ***
## fit_P       -0.822084   0.024308 -33.8196 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## RMSE: 0.239465   Adj. R2: 0.801948
## F-test (1st stage), P: stat = 2,449.56, p < 2.2e-16, on 1 and 598 DoF.
##            Wu-Hausman: stat =   542.56, p < 2.2e-16, on 1 and 597 DoF.

Caveats.

2SLS regression analysis can be very insightful, but I also want to stress some caveats about their practical application. Most of which stem directly from the absence of control that true experiments have.

Instrument exogeneity (Exclusion Restriction): The instrument must affect outcomes only through the treatment variable (e.g., only supply is affected directly, not demand).
Instrument relevance: The instrument must be strongly correlated with the endogenous regressor, implying the shock creates meaningful variation.
Functional form correctness: Supply and demand are assumed linear and additively separable.
Multiple hypothesis testing risks: We were not repeatedly testing different instruments, which can artificially produce significant findings by chance.
Exclusion restriction violations: Spatial or temporal spillovers may cause instruments to affect the outcome through unintended channels, undermining instrument exogeneity.
Weak instruments: Spatial clustering, serial correlation, or network interdependencies can reduce instrument variation, causing weak instruments.
Inference and standard errors: Spatial or temporal interdependence reduces the effective sample size, making conventional standard errors misleadingly small.

We always get coefficients back when running feols, and sometimes the computed p-values are very small. The interpretation of those numbers rests on many assumptions, and we are rarely sure that all of these assumptions hold. Researchers often also report their OLS results, but that is insufficient.

20.4 Further Reading

You are directed to the following resources which discusses endogeneity in more detail and how it applies generally.

Causal Inference for Statistics, Social, and Biomedical Sciences: An Introduction
https://www.mostlyharmlesseconometrics.com/
https://www.econometrics-with-r.org
https://bookdown.org/paul/applied-causal-analysis/
https://mixtape.scunning.com/
https://theeffectbook.net/
https://www.r-causal.org/
https://matheusfacure.github.io/python-causality-handbook/landing-page.html

For RDD and DID methods in natural experiments, see

For IV methods in natural experiments, see

Notice that even in this linear model, however, all effects are conditional: The effect of a cost change on quantity or price depends on the demand curve. A change in costs affects quantity supplied but not quantity demanded (which then affects equilibrium price) but the demand side of the market still matters! The change in price from a change in costs depends on the elasticity of demand.↩︎
Mathematically, we can also do this in a single step by exploiting linear algebra: \(\frac{\frac{ Cov(Q^{*},\alpha_{S})}{ V(\alpha_{S}) } }{\frac{ Cov(P^{*},\alpha_{S})}{ V(\alpha_{S}) }} = \frac{Cov(Q^{*},\alpha_{S} )}{ Cov(P^{*},\alpha_{S})}.\)↩︎