We now consider a bivariate random vector \((X_{i}, Y_{i})\), which is a theoretical version of the bivariate observations \((\hat{X}_{i}, \hat{Y}_{i})\). E.g., If we are going to flip two coins, then \((X_{i}, Y_{i})\) corresponds to the unflipped coins and \((\hat{X}_{i}, \hat{Y}_{i})\) corresponds to concrete values after they are flipped.
The joint distribution is defined as \[\begin{eqnarray} Prob(X_{i} = x, Y_{i} = y) \end{eqnarray}\] For example, consider a bivariate random vector with three outcomes for \(X_{i}\) and three outcomes for \(Y_{i}\). The plot below shows each outcome \((x,y)\) with deeper colors reflecting higher probability events.
prob_table <- expand.grid(x=c(0,1,2), y=c(0,10,20))
prob_table[,'probabilities'] <- c(
0.0, 0.1, 0.0,
0.1, 0.3, 0.1,
0.1, 0.2, 0.2)
plot(prob_table[,'x'], prob_table[,'y'],
xlim=c(-0.5,2.5), ylim=c(-5, 25),
pch=21, cex=8, col='blue',
bg=rgb(0,0,1, prob_table[,'probabilities']),
xlab = "X", ylab = "Y")
Note that variables are statistically independent if \(Prob(X_{i} = x, Y_{i} = y)= Prob(X_{i} = x) Prob(Y_{i} = y)\) for all \(x, y\). Independence is sometimes assumed for mathematical simplicity, not because it generally fits data well.1
The conditional distributions are defined as \[\begin{eqnarray} Prob(X_{i} = x | Y_{i} = y) = \frac{ Prob(X_{i} = x, Y_{i} = y)}{ Prob( Y_{i} = y )}\\ Prob(Y_{i} = y | X_{i} = x) = \frac{ Prob(X_{i} = x, Y_{i} = y)}{ Prob( X_{i} = x )} \end{eqnarray}\] The marginal distributions are then defined as \[\begin{eqnarray} Prob(X_{i} = x) = \sum_{y} Prob(X_{i} = x | Y_{i} = y) Prob( Y_{i} = y ) \\ Prob(Y_{i} = y) = \sum_{x} Prob(Y_{i} = y | X_{i} = x) Prob( X_{i} = x ), \end{eqnarray}\] which is also known as the law of total probability.
For one example, Consider flipping two coins, where we mark whether “heads” is face up with a \(1\) and “tail” with a \(0\). E.g., the first coin has a value of \(x=1\) if it shows heads and \(x=0\) if it shows tails. This table shows both the joint distribution and also each marginal distribution.
| \(x=0\) | \(x=1\) | Marginal | |
|---|---|---|---|
| \(y=0\) | \(Prob(X_{i}=0,Y_{i}=0)\) | \(Prob(X_{i}=1,Y_{i}=0)\) | \(Prob(Y_{i}=0)\) |
| \(y=1\) | \(Prob(X_{i}=0,Y_{i}=1)\) | \(Prob(X_{i}=1,Y_{i}=1)\) | \(Prob(Y_{i}=1)\) |
| Marginal | \(Prob(X_{i}=0)\) | \(Prob(X_{i}=1)\) | \(1\) |
Note that different joint distributions can have the same marginal distributions.
The joint distribution is defined as \[\begin{eqnarray} F(x, y) &=& Prob(X_{i} \leq x, Y_{i} \leq y) \end{eqnarray}\] The marginal distributions are then defined as \[\begin{eqnarray} F_{X}(x) &=& F(x, \infty)\\ F_{Y}(y) &=& F(\infty, y). \end{eqnarray}\] which is also known as the law of total probability. Variables are statistically independent if \(F(x, y) = F_{X}(x)F_{Y}(y)\) for all \(x, y\).
For example, suppose \((X_{i},Y_{i})\) is bivariate normal with means \((\mu_{X}, \mu_{Y})\), variances \((\sigma_{X}, \sigma_{Y})\) and covariance \(\rho\).
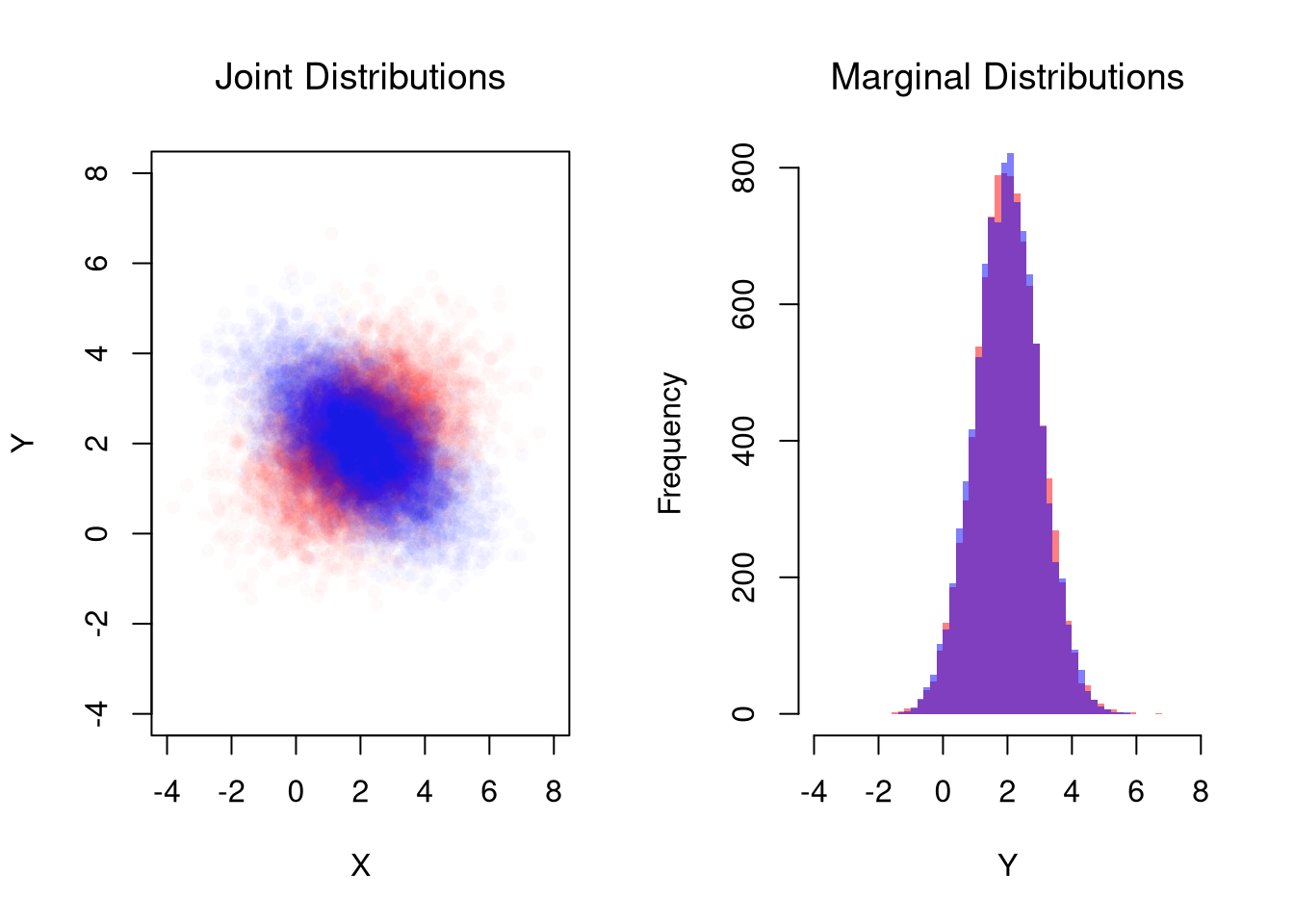
# Simulate Bivariate Data
N <- 10000
Mu <- c(2,2) ## Means
Sigma1 <- matrix(c(2,-.8,-.8,1),2,2) ## CoVariance Matrix
MVdat1 <- mvtnorm::rmvnorm(N, Mu, Sigma1)
colnames(MVdat1) <- c('X','Y')
Sigma2 <- matrix(c(2,.4,.4,1),2,2) ## CoVariance Matrix
MVdat2 <- mvtnorm::rmvnorm(N, Mu, Sigma2)
colnames(MVdat2) <- c('X','Y')
par(mfrow=c(1,2))
## Different diagonals
plot(MVdat2, col=rgb(1,0,0,0.02), pch=16,
main='Joint Distributions', font.main=1,
ylim=c(-4,8), xlim=c(-4,8),
xlab='X', ylab='Y')
points(MVdat1,col=rgb(0,0,1,0.02),pch=16)
## Same marginal distributions
xbks <- seq(-4,8,by=.2)
hist(MVdat2[,2], col=rgb(1,0,0,0.5),
breaks=xbks, border=NA,
xlab='Y',
main='Marginal Distributions', font.main=1)
hist(MVdat1[,2], col=rgb(0,0,1,0.5),
add=T, breaks=xbks, border=NA)
# See that independent data are a special case
n <- 2e4
## 2 Indepenant RV
XYiid <- cbind( rnorm(n), rnorm(n))
## As a single Joint Draw
XYjoint <- mvtnorm::rmvnorm(n, c(0,0))
## Plot
par(mfrow=c(1,2))
plot(XYiid, xlab=
col=grey(0,.05), pch=16, xlim=c(-5,5), ylim=c(-5,5))
plot(XYjoint,
col=grey(0,.05), pch=16, xlim=c(-5,5), ylim=c(-5,5))
# Compare densities
#d1 <- dnorm(XYiid[,1],0)*dnorm(XYiid[,2],0)
#d2 <- mvtnorm::dmvnorm(XYiid, c(0,0))
#head(cbind(d1,d2))The multivariate normal is a workhorse for analytical work on multivariate random variables, but there are many more. See e.g., https://cran.r-project.org/web/packages/NonNorMvtDist/NonNorMvtDist.pdf
Also note Bayes’ Theorem: \[\begin{eqnarray} Prob(X_{i} = x | Y_{i} = y) Prob( Y_{i} = y) &=& Prob(X_{i} = x, Y_{i} = y) = Prob(Y_{i} = y | X_{i} = x) Prob(X_{i} = x).\\ Prob(X_{i} = x | Y_{i} = y) &=& \frac{ Prob(Y_{i} = y | X_{i} = x) Prob(X_{i}=x) }{ Prob( Y_{i} = y) }. \end{eqnarray}\]
# Verify Bayes' theorem for the unfair coin case:
# Compute Prob(X1=1 | X2=1) using the formula:
# Prob(X1=1 | X2=1) = [Prob(X2=1 | X1=1) * Prob(X1=1)] / Prob(X2=1)
P_X1_1 <- 0.5
P_X2_1_given_X1_1 <- 1 # Since coin 2 copies coin 1.
P_X2_1 <- P_X2_unfair["X2=1"]
bayes_result <- (P_X2_1_given_X1_1 * P_X1_1) / P_X2_1
bayes_result
## X2=1
## 1We will now dig a little deeper theoretically into the statistics we compute. When we know how the data are generated theoretically, we can often compute the theoretical value of the most basic and often-used bivariate statistic: the Pearson correlation. To see this, we focus on two discrete random variables, first showing their covariance, \(\mathbb{C}[X_{i}, Y_{i}]\), and then their correlation \(\mathbb{R}[X_{i}, Y_{i}]\). Referring to and \(\mu_{X}=\mathbb{E}[X_{i}]\) and \(\mu_{Y}=\mathbb{E}[Y_{i}]\), we have \[\begin{eqnarray} \mathbb{C}[X_{i}, Y_{i}] &=& \mathbb{E}[(X_{i} – \mu_{X})(Y_{i} – \mu_{Y}])] = \sum_{x}\sum_{y} (x – \mu_{X})(y – \mu_{Y}) Prob(X_{i} = x, Y_{i} = y) \\ \mathbb{R}[X_{i}, Y_{i}] &=& \frac{\mathbb{C}[X_{i}, Y_{i}] }{ \sqrt{\mathbb{V}[X_{i}]} \sqrt{\mathbb{V}[Y_{i}]} } \end{eqnarray}\]
For example, suppose we have discrete data with the following outcomes and probabilities. Note that cells reflect the probabilities of the outcomes depicted on the row and column labels, e.g. \(Prob(X_{i}=1, Y_{i}=0)=0.1\).
| \(x=0\) | \(x=1\) | \(x=2\) | |
|---|---|---|---|
| \(y=0\) | \(0.0\) | \(0.1\) | \(0.0\) |
| \(y=10\) | \(0.1\) | \(0.3\) | \(0.1\) |
| \(y=20\) | \(0.1\) | \(0.1\) | \(0.2\) |
After verifying that the probabilities sum to \(1\), we then compute the marginal distributions \[\begin{eqnarray} Prob(X_{i}=0)=0.2,\quad Prob(X_{i}=1)=0.5,\quad Prob(X_{i}=2) = 0.3 \\ Prob(Y_{i}=0)=0.1,\quad Prob(Y_{i}=10)=0.5,\quad Prob(Y_{i}=20) = 0.4 \end{eqnarray}\] which allows us to compute the means: \[\begin{eqnarray} \mathbb{E}[X_{i}] &=& 0(0.2)+1(0.5)+2(0.3) = 1.1 \\ \mathbb{E}[Y_{i}] &=& 0(0.1)+10(0.5)+20(0.4) = 13 \end{eqnarray}\] We can then compute the cell-by-cell contributions: \(Prob(X_{i} = x, Y_{i} = y) (x-\mathbb{E}[X_{i}])(y-\mathbb{E}[Y_{i}])\), which lead plug in to the covariance formula; \[\begin{eqnarray} \begin{array}{l l r r r r r} \hline x & y & Prob(X_{i}=x, Y_{i}=y) & x-\mathbb{E}[X_{i}] & y-\mathbb{E}[Y_{i}] & (x-\mathbb{E}[X_{i}])(y-\mathbb{E}[Y_{i}]) & \text{Contribution}\\ \hline 0 & 0 & 0.0 & -1.1 & -13 & 14.3 & 0\\ 0 & 10 & 0.1 & -1.1 & -3 & 3.3 & 0.330\\ 0 & 20 & 0.1 & -1.1 & 7 & -7.7 & -0.770\\ 1 & 0 & 0.1 & -0.1 & -13 & 1.3 & 0.130\\ 1 & 10 & 0.3 & -0.1 & -3 & 0.3 & 0.090\\ 1 & 20 & 0.1 & -0.1 & 7 & -0.7 & -0.070\\ 2 & 0 & 0.0 & 0.9 & -13 & -11.7 & 0\\ 2 & 10 & 0.1 & 0.9 & -3 & -2.7 & -0.270\\ 2 & 20 & 0.2 & 0.9 & 7 & 6.3 & 1.260\\ \hline \end{array} \end{eqnarray}\] \[\begin{eqnarray} \mathbb{C}[X_{i},Y_{i}] &=& \sum_{x} \sum_{y} \left(x-\mathbb{E}[X_{i}]\right)\left(y-\mathbb{E}[Y_{i}]\right) Prob\left(X_{i} = x, Y_{i} = y\right) \\ &=& 0 + 0.330 -0.770 + 0.130 + 0.090 -0.070 +0 -0.270 + 1.260 = 0.7 \end{eqnarray}\]
To compute the correlation value, we first need the standard deviations \[\begin{eqnarray} \mathbb{V}[X_{i}] &=& \sum_{x} (x-\mathbb{E}[X_{i}])^2 Prob(X_{i} = x) \\ &=& (0-1.1)^2(0.2)+(1-1.1)^2(0.5)+(2-1.1)^2(0.3)=0.49 \\ \mathbb{V}[Y_{i}] &=& \sum_{y} (y-\mathbb{E}[Y_{i}])^2 Prob(Y_{i} = y) \\ &=& (0-13)^2(0.1)+(10-13)^2(0.5)+(20-13)^2(0.4)=41 \\ \end{eqnarray}\] Then we can find the correlation as \[\begin{eqnarray} \frac{\mathbb{C}[X_{i},Y_{i}]}{ \sqrt{\mathbb{V}[X_{i}]} \sqrt{\mathbb{V}[Y_{i}]} } &=& \frac{0.7}{\sqrt{0.49} \sqrt{41}} \approx 0.156, \end{eqnarray}\] which suggests a weak positive association between the variables.
Note that you can do all of the above calculations using the computer instead of by hand.
# Make a Probability Table
x <- c(0,1,2)
y <- c(0,10,20)
xy_probs <- matrix(c(
0.0, 0.1, 0.0,
0.1, 0.3, 0.1,
0.1, 0.1, 0.2
), nrow=3, ncol=3, byrow=TRUE)
rownames(xy_probs) <- paste0('y=',y)
colnames(xy_probs) <- paste0('x=',x)
xy_probs
## x=0 x=1 x=2
## y=0 0.0 0.1 0.0
## y=10 0.1 0.3 0.1
## y=20 0.1 0.1 0.2
# Compute Marginals and Means
pX <- colSums(xy_probs)
pY <- rowSums(xy_probs)
EX <- sum(x * pX)
EY <- sum(y * pY)
# Compute Covariance
dxy_grid <- expand.grid(dy=y-EY, dx=x-EX)[,c(2,1)]
dxy_grid[,'p'] <- as.vector(xy_probs)
dxy_grid[,'contribution'] <- dxy_grid[,'dx'] * dxy_grid[,'dy'] * dxy_grid[,'p']
CovXY <- sum(dxy_grid[,'contribution'])
CovXY
## [1] 0.7
# Compute Variances
VX <- sum( (x-EX)^2 * pX)
SX <- sqrt(VX)
VY <- sum( (y-EY)^2 * pY)
SY <- sqrt(VY)
# Compute Correlation
CorXY <- CovXY / (SX * SY)
CorXY
## [1] 0.1561738Many introductory econometrics textbooks have a good appendix on probability and statistics. There are many useful statistical texts online too
See the Further reading about Probability Theory in the Statistics chapter.
The same can be said about assuming normally distributed errors, although at least that can be motivated by the Central Limit Theorems.↩︎