3 Numerical Statistics

We often summarize distributions with statistics: functions of data. We will go through some specific examples mathematically below, but can intuitively understand that they are generally computed as statistic <- function(x){ .... }.

Tip

Note that functions can take functions as arguments, meaning we can also program statistics generally as

Code

statistic <- function(X, f){
    y <- f(X)
    return(y)
}

X <- c(0,1,3,10,6) # Data
statistic(X, sum)
## [1] 20

The most basic way to compute statistics is with summary, which reports multiple values that can all be calculated individually.

Code

# A random sample (real data)
X <- USArrests[,'Murder']
summary(X)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   0.800   4.075   7.250   7.788  11.250  17.400

# A random sample (computer simulation)
X <-  runif(1000)
summary(X)
##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
## 0.001442 0.250637 0.509871 0.501544 0.742488 0.999849

# Another random sample (computer simulation)
X <- rnorm(1000) 
summary(X)
##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
## -3.39150 -0.69232  0.01046 -0.01267  0.63230  3.09302

Together, the sample mean and variance statistics summarize the central tendency and dispersion of a distribution. In some special cases, such as with the normal distribution, they completely describe the distribution. Other distributions are better described with other statistics, either as an alternative or in addition to the mean and variance. After discussing those other statistics, we will return to the two most basic statistics in theoretical detail.

3.1 Mean and Variance

The mean and variance are the two most basic statistics that summarize the center and how spread apart the values are for data in your sample. As before, we represent data as vector \(\hat{X}=(\hat{X}_{1}, \hat{X}_{2}, ....\hat{X}_{n})\), where there are \(n\) observations and \(\hat{X}_{i}\) is the value of the \(i\)th one.

Mean.

Perhaps the most common statistic is the empirical mean, also known as the sample mean, which is the [sum of all values] divided by [number of values]; \[\begin{eqnarray} \hat{M} &=& \frac{\sum_{i=1}^{n}\hat{X}_{i}}{n}, \end{eqnarray}\] where \(\hat{X}_{i}\) denotes the value of the \(i\)th observation.

Note

For example, a dataset of \(\{1,4,10\}\) has a mean of \([1+4+10]/3=5\).

Code

X <- c(1,4,10)
sum(X)/length(X)
## [1] 5
mean(X)
## [1] 5

Code

# compute the mean of a random sample
X1 <- USArrests[,'Murder']
X1_mean <- mean(X1)
X1_mean
## [1] 7.788

# visualize on a histogram
hist(X1, border=NA, main=NA, freq=F,)
abline(v=X1_mean, col=2, lwd=2)
title(paste0('mean= ', round(X1_mean,2)), font.main=1)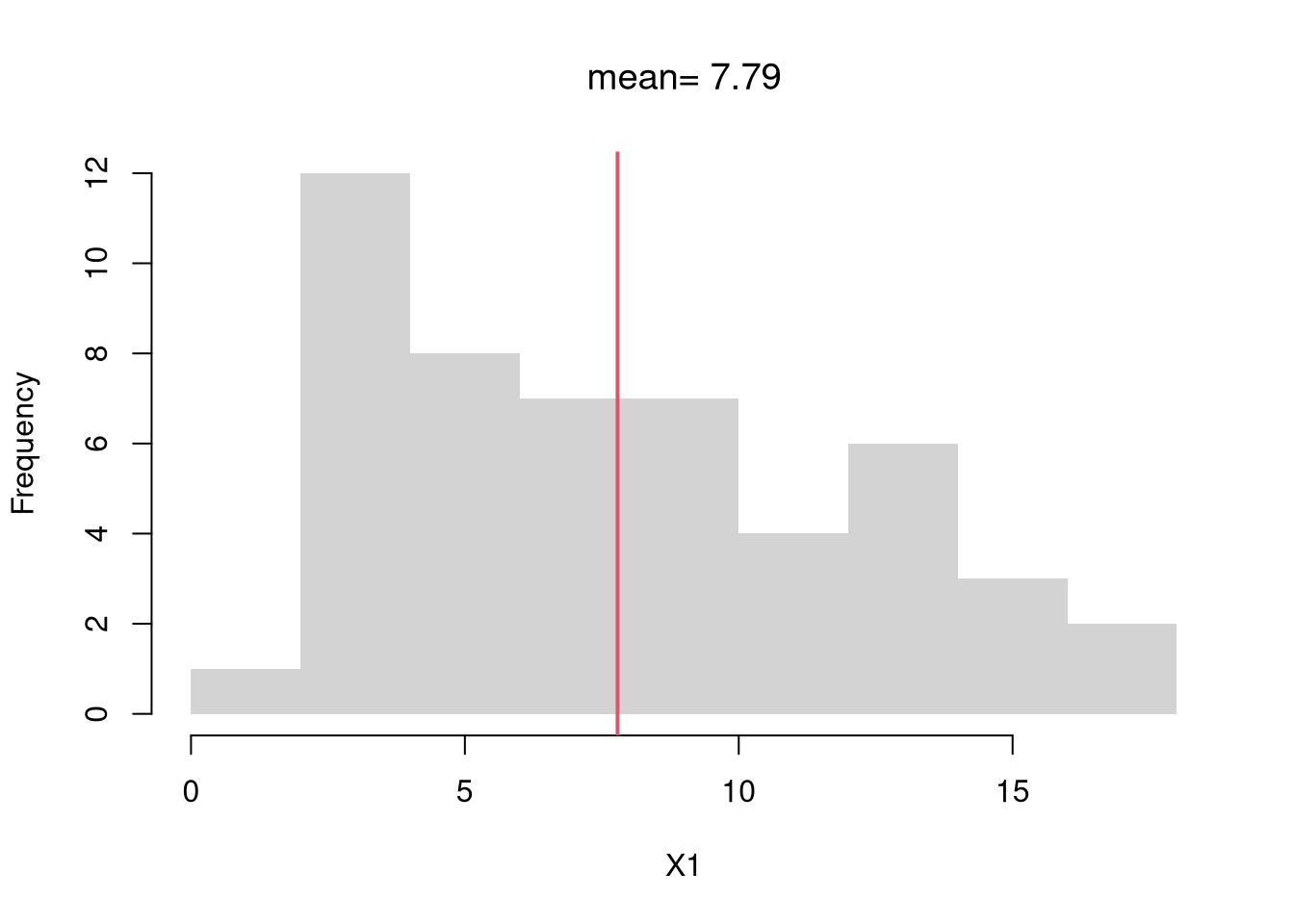

Variance.

Perhaps the second most common statistic is the empirical variance: the average squared deviation from the mean \[\begin{eqnarray} \hat{V} &=&\frac{\sum_{i=1}^{n} [\hat{X}_{i} - \hat{M}]^2}{n}. \end{eqnarray}\] The empirical standard deviation is simply \(\hat{S} = \sqrt{\hat{V} }\).

Note

For example, a dataset of \(\{1,4,10\}\) has a mean of \([1+4+10]/3=5\). The variance is \([(1-5)^2+(4-5)^2+(10-5)^2]/3=[16+1+25]/3=42/3=14\) and the standard deviation is \(\sqrt{14}\).

Code

X <- c(1,4,10)
X_mean <- mean(X)
X_var <- mean( (X - X_mean)^2 )
sqrt(X_var)
## [1] 3.741657

Code

X1_s <- sd(X1) # sqrt(var(X))
hist(X1, border=NA, main=NA, freq=F)
X1_s_lh <- c(X1_mean - X1_s,  X1_mean + X1_s)
abline(v=X1_s_lh, col=4)
text(X1_s_lh, -.02,
    c( expression(bar(X)-s[X]), expression(bar(X)+s[X])),
    col=4, adj=0)
title(paste0('sd= ', round(X1_s,2)), font.main=1)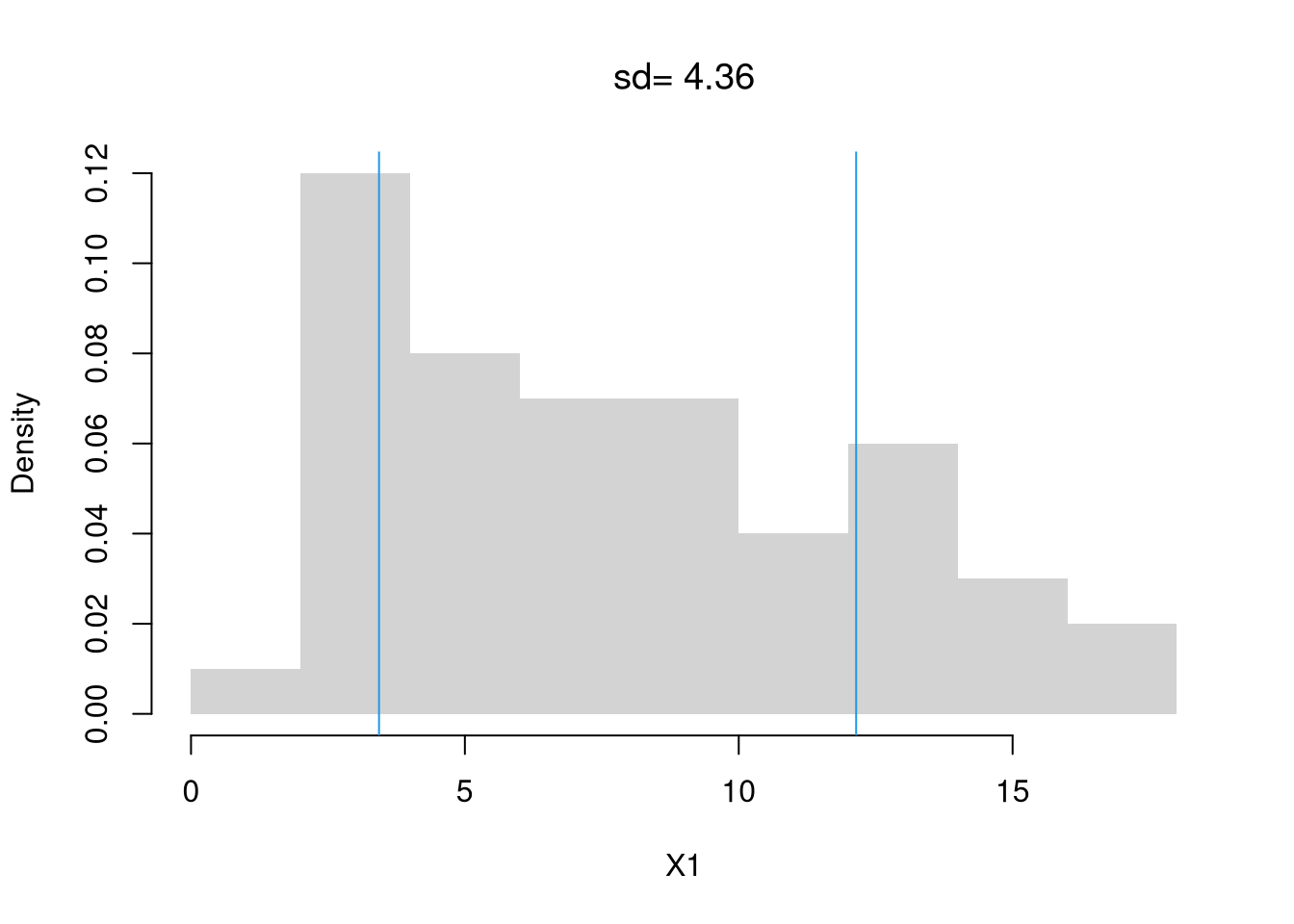

Tip

Note that a “unbiased version” of the empirical variance is used by R and many statisticians: \(\hat{V}' =\frac{\sum_{i=1}^{n} [\hat{X}_{i} - \hat{M}]^2}{n-1}\) and \(\hat{S}' = \sqrt{\hat{V}'}\). In this class, we use the version defined previously because we do not yet know about “bias/unbiased” statistics. Do not be concerned, as there is hardly any difference when \(n\) is large: e.g., \(\frac{1}{n}\approx \frac{1}{n-1}\) for \(n=100,000\).

Code

X <- c(1,4,10)

X_mean <- mean(X)
X_var <- mean( (X - X_mean)^2 )
X_var
## [1] 14

# Corrected Version
n <- length(X)  
X_var2 <- sum( (X - X_mean)^2 )/(n-1)
X_var2
## [1] 21

var(X) # R-Version
## [1] 21

3.2 Other Center/Spread Statistics

A general rule of applied statistics is that there are multiple ways to measure something. Mean and Variance are measurements of Center and Spread, but there are others that have different theoretical properties and may be better suited for your dataset.

Medians and Absolute Deviations.

We can use the empirical Median as a “robust alternative” to means that is especially useful for data with asymmetric distributions and extreme values. Recall that the \(q\)th quantile is the value where \(q\) percent of the data are below and (\(1-q\)) percent are above. The median (\(q=.5\)) is the point where half of the data is lower values and the other half is higher. This implies that median is not sensitive to extreme values (whereas the mean is).

Code

X1 <- USArrests[,'Murder']
median(X1)
## [1] 7.25
quantile(X1, prob=0.5)
##  50% 
## 7.25

Note

Examine robustness to an extreme value

Code

X1_extreme <- c(X1, 1000) # add one extreme value
#par(mfrow=c(1,2)) # visualize side-by-side
#hist(X1)
#hist(X1_extreme)

# Which measures of central tendency are robust
# to a single extreme value?
mean( X1)
## [1] 7.788
mean( X1_extreme )
## [1] 27.24314

quantile(X1, prob=0.5)
##  50% 
## 7.25
quantile(X1_extreme, prob=0.5)
## 50% 
## 7.3

We can also use the sample Interquartile Range or Median Absolute Deviation as an alternative to variance. The difference between the first and third quartiles (quantiles \(q=.25\) and \(q=.75\)) measure is range of the middle \(50%\) of the data, which is how the boxplot measures “spread”. The median absolute deviation is another statistic that also measures “spread”. \[\begin{eqnarray} \tilde{M} &=& \text{Med}( \hat{X}_{i}) \\ \hat{\text{MAD}} &=& \text{Med}\left( | \hat{X}_{i} - \tilde{M} | \right). \end{eqnarray}\]

Code

IQR(X1)
## [1] 7.175
mad(X1)
## [1] 5.41149

Note

Compute the \(IQR\) statistic for the dataset \(\{-100,1,4,10,10\}\).

\(IQR =\) Upper quartile \(-\) Lower quartile \(= 10 - 1 = 9\).

Code

X <- c(1,4,10)
# An intuitive alternative to sd(X), used in the boxplot
quants <- quantile(X, probs=c(.25,.75))
quants[2]-quants[1]
## 75% 
## 4.5
IQR(X)
## [1] 4.5

Compute the \(\text{MAD}\) statistic for the dataset \(\{1,4,10\}\). First compute the median, \(\text{Med}(1,4,10)=4\). Then compute \(\text{Med}( |1-4|,~ |4-4|,~ |10-4| )= \text{Med}( 3, 0, 6 ) = 3\).

Code

#Another alternative to sd(X)
mad(X, constant=1)
## [1] 3

# Computationally equivalent
# x_med <- quantile(X, probs=.5)
# x_absdev <- abs(X -x_med)
# quantile(x_absdev, probs=.5)

Note

Compare the robustness of various “spread” metrics to an extreme value

Code

sd(X1)
## [1] 4.35551
sd(X1_extreme)
## [1] 139.0044

IQR(X1)
## [1] 7.175
IQR(X1_extreme)
## [1] 7.2

mad(X1, constant=1)
## [1] 3.65
mad(X1_extreme, constant=1)
## [1] 3.8

Tip

Note that there other “absolute deviation” statistics

Code

# sometimes seen elsewhere
mean( abs(X1 - mean(X1)) )
mean( abs(X1 - median(X1)) )

Weighted Statistics.

The mean generalizes to a weighted mean: an average where different values contribute to the final result with varying levels of importance. For each outcome \(x\) we have a weight \(W_{x}\) and compute \[\begin{eqnarray} \hat{M} &=& \frac{\sum_{x} x W_{x}}{\sum_{x} W_{x}} = \sum_{x} x w_{x}, \end{eqnarray}\] where \(w_{x}=\frac{W_{x}}{\sum_{x'} W_{x'}}\) is normalized version of \(W_{x}\) that implies \(\sum_{x}w_{x}=1\).

Note

For another example, suppose a student has these scores

Code

Homework1 <- c(score=88, weight=0.25)
Homework2 <- c(score=92, weight=0.25)
Exam1 <- c(score=67, weight=0.2)
Exam2 <- c(score=90, weight=0.3)

Grades <- rbind(Homework1, Homework2, Exam1, Exam2)
Grades
##           score weight
## Homework1    88   0.25
## Homework2    92   0.25
## Exam1        67   0.20
## Exam2        90   0.30

We can compute the final grade as a weighted mean

Code

# Manual Way
88*0.25 + 92*0.25 + 67*0.2 + 90*0.3
## [1] 85.4

# Computerized Way
Values <- Grades[,'score'] * Grades[,'weight']
FinalGrade <- sum(Values)
FinalGrade
## [1] 85.4

When data are discrete, we can also compute the mean using “probability weights” \(w_{x} = \hat{p}_{x}=\sum_{i=1}^{n}\mathbf{1}\left(\hat{X}_{i}=x\right)/n\).

Note

E.g., the dataset \(\{1,2,1,3,1\}\) has \(\hat{p}_{1}=\frac{3}{5}\), \(\hat{p}_{2}=\frac{1}{5}\), \(\hat{p}_{3}=\frac{1}{5}\). Then, sorting the dataset as {1,1,1,2,3}, we can see that \(\hat{M} = [1+1+1+2+2+3]/5 = [1+1+1]/5 + [2+2]/5+ 3/5 = 1 \frac{3}{5} + 2 \frac{3}{5} + 3 \frac{1}{5} = 1 \hat{p}_{1} + 2 \hat{p}_{2} + 3 \hat{p}_{3}\). In either case, we end up with \(\frac{3+6+3}{5}=12/5=1.6\)

Code

X <- c(1,2,1,3,1)
mean(X)
## [1] 1.6

proportions <- table(X)/length(X)
proportions
## X
##   1   2   3 
## 0.6 0.2 0.2
vals <- sort(unique(X))
sum(vals*proportions)
## [1] 1.6

In principle, we can also compute other weighted statistics such as a weighted median.

Tip

See that we can also compute weighted quantiles

Code

weighted.quantile <- function(x, w, probs){
    #See spatstat.univar::weighted.quantile
    oo <- order(x)
    x <- x[oo]
    w <- w[oo]
    Fx <- cumsum(w)/sum(w)
    quantile_id <- max(which(Fx <= probs))+1
    xq <- x[quantile_id] 
    return(xq)
}

## Unweighted
quantile(X, probs=.5)
## 50% 
##   1
weights <- rep(1, length(X))
weighted.quantile(x=X, w=weights, probs=.5)
## [1] 1

## Weighted
weights <- seq(X)
weights <- weights/sum(weights) # normalize
weighted.quantile(x=X, w=weights, probs=.5)
## [1] 1

Mode and Share Concentration.

Sometimes, none of the above work well. With categorical data, for example, distributions are easier to describe with other statistics. The sample mode is the most common observation: the value with the highest observed frequency. We can also measure the spread of the frequencies or concentration at the mode vs elsewhere.

Tip

Here is an example of the mode. Notice it is not the middle letter.

Code

X <- c('A', 'B', 'A', 'C', 'C', 'A')
proportions <- table(X)/length(X)
plot(proportions, col=grey(0,0.5))

Code


# mode(s)
mode_id <- which(proportions==max(proportions))
names(proportions)[ mode_id ]
## [1] "A"

Here is an example of spread for categorical data.

Code

# freq. spreads
sd(proportions)
## [1] 0.1666667
sum(proportions^2)
## [1] 0.3888889

# freq. concentration at mode
max(proportions)/mean(proportions)
## [1] 1.5

3.3 Shape Statistics

Central tendency and dispersion are often insufficient to describe a distribution. To further describe shape, we can compute sample skew and kurtosis to measure asymmetry and extreme values.

There are many other statistics we could compute on an ad-hoc basis. However, shape is often best understood with graphical descriptions: histogram, ECDF, Boxplot. These should be made before numerical descriptions: skewness and kurtosis statistics.

Skewness.

The skewness statistic captures how asymmetric the distribution is by measuring the average cubed deviation from the mean, normalized the standard deviation cubed \[\begin{eqnarray} \frac{\sum_{i=1}^{n} [\hat{X}_{i} - \hat{M}]^3 / n}{ \hat{S}^3 } \end{eqnarray}\]

Code

X <- USArrests[,'Murder']
hist( X^2, border=NA, 
    xlab='[Murder Rate]^2',
    main=NA, freq=F, breaks=20)

Code


skewness <-  function(X){
 X_mean <- mean(X)
 m3 <- mean((X - X_mean)^3)
 s3 <- sd(X)^3
 skew <- m3/s3
 return(skew)
}

skewness( X^2 )
## [1] 1.078254
skewness( X^3 )
## [1] 1.658012

We can automatically compare against the normal distribution, which has a skew of 0.

Kurtosis.

This statistic captures how many “outliers” there are like skew but looking at quartic deviations instead of cubed ones. \[\begin{eqnarray} \frac{\sum_{i=1}^{n} [\hat{X}_{i} - \hat{M}]^4 / n}{ \hat{S}^4 }. \end{eqnarray}\] Some authors further subtract \(3\) to explicitly compare against the normal distribution (the normal distribution has a kurtosis of \(3\)).

Boxplot whiskers are a great way to examine kurtosis, with more circle ``outliers’’ indicating more kurtosis. You can also see skew in the boxplot when one quartile is much further from the median than the other.

Code

X1 <- X^1/mean(X^1)
X2 <- X^2/mean(X^2)
X3 <- X^3/mean(X^3)
X4 <- X^4/mean(X^4)
boxplot(X1, X2, X3, X4,
    names=c(1,2,3,4), xlab='Data Transformations',
    main=NA)

Code



kurtosis <- function(X){  
 X_mean <- mean(X)
 m4 <- mean((X - X_mean)^4) 
 s4 <- sd(X)^4
 kurt <- m4/s4
 return(kurt)
 # use instead to compare against normal
 # excess_kurt <- kurt - 3 
}

kurtosis( X1 )
## [1] 2.05077
kurtosis( X2 )
## [1] 3.247877
kurtosis( X3 )
## [1] 5.166225
kurtosis( X4 )
## [1] 7.511867

Clusters/Gaps.

You can also describe distributions in terms of how clustered the values are, including the number of modes, bunching, and many other statistics. But remember that “a picture is worth a thousand words”.

3.4 Data Transformations

Transformations can stabilize variance, reduce skewness, and make model errors closer to Gaussian.

Perhaps the most common examples are power transformations: \(y= x^\lambda\), which includes \(\sqrt{x}\) and \(x^2\).

Other examples include the exponential transformation: \(y=\exp(x)\) for any \(x\in (-\infty, \infty)\) and logarithmic transformation: \(y=\log(x)\) for any \(x>0\).

Tip

The exponential function is \(e^{x}=1+x/1+2^2/2+x^3/6....=\sum_{k=0}^{\infty} x^k/k!\) and the \(log\) function is it’s inverse.

Code

x <- 1:4

y <- exp(x)
y
## [1]  2.718282  7.389056 20.085537 54.598150

z <- log(y)
z
## [1] 1 2 3 4

The Box–Cox Transform nests many cases used by statisticians. For \(x>0\) and parameter \(\lambda\), \[\begin{eqnarray} y=\begin{cases} \dfrac{x^\lambda-1}{\lambda}, & \lambda\neq 0,\\ \log\left(x\right) & \lambda=0. \end{cases} \end{eqnarray}\] This function is continuous over \(\lambda\).

Code

# Box–Cox transform and inverse
bc_transform <- function(x, lambda) {
  if (any(x <= 0)) stop("Box-Cox requires x > 0")
  if (abs(lambda) < 1e-8) log(x) else (x^lambda - 1)/lambda
}
bc_inverse <- function(t, lambda) {
  if (abs(lambda) < 1e-8) exp(t) else (lambda*t + 1)^(1/lambda)
}

X <- USArrests[,'Murder']
hist(X, main='', border=NA, freq=F)

Code


par(mfrow=c(1,3))
for(lambda in c(-1,0,1)){
    Y <- bc_transform(X, lambda)
    hist(Y, 
        main=bquote(paste(lambda,'=',.(lambda))),
        border=NA, freq=F)
}

Be careful about transforming your data, as the interpretation can be harder.

The mean of transformed data is not equivalent to transforming the mean, for example, which is one reason why you want to first summarize your data before transforming it.

Jensen’s inequality.

We can actually say more about how the mean of transformed data not equivalent to transforming the mean. To do that, we define two types of functions:

Concave functions curve inwards, like the inside of a cave.
Convex functions curve outward, the opposite of concave.

Let \(\hat{Y}_{i}=g( \hat{X}_{i})\), and denote the mean as \(\hat{M}_{Y}\).

If \(g\) is a concave function, then \(g( \hat{M}_{X} ) \geq \hat{M}_{Y}\).

Tip

Here are some examples.

Code

# Continuous Example 1
x <- c(0, 1.123, 2.987, 3.654)
mean( sqrt(x) )
## [1] 1.174889
sqrt( mean(x) ) 
## [1] 1.393198

# Continuous Example 2
mean( log(x) )
## [1] -Inf
log( mean(x) ) 
## [1] 0.6632033

Code

## Discrete Example
x  <- c(1,2,3)
px <- c(0.2,0.5,0.3)
MX <- sum(x * px)
MX
## [1] 2.1

g  <- sqrt
g(MX)
## [1] 1.449138

MY <- sum(g(x) * px)
MY
## [1] 1.426722

If \(g\) is a convex function, then the inequality reverses: \(g( \hat{M}_{X}) \leq \hat{M}_{Y}\).

Code

mean( exp(x) )
## [1] 10.06429
exp( mean(x) )  
## [1] 7.389056